a) Xét \(f(x) = 2{x^3} - 9{x^2} + 12x + 1\) trên đoạn [0;3]
\(f'(x) = 6{x^2} - 18x + 12 = 0 \Leftrightarrow \left[ \begin{array}{l}x = 2\\x = 1\end{array} \right.\)
Bảng biến thiên:
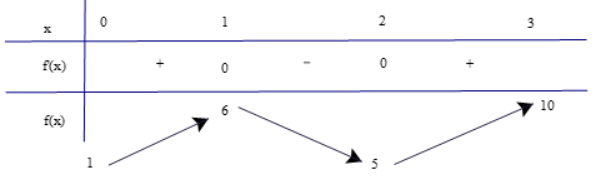
Từ bảng biến thiên, ta thấy \(\mathop {\min }\limits_{[0;3]} f(x) = f(0) = 1\) và \(\mathop {\max }\limits_{[0;3]} f(x) = f(3) = 10\)
b) Xét \(g(x) = x + \frac{1}{x}\) trên khoảng (0;5)
\(g'(x) = 1 - \frac{1}{{{x^2}}} = 0 \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = - 1(loai)\end{array} \right.\)
Bảng biến thiên:
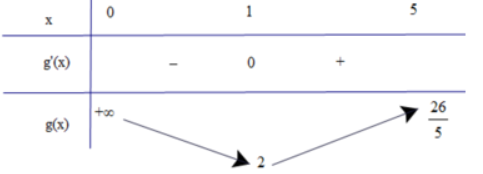
Từ bảng biến thiên, ta thấy \(\mathop {\min }\limits_{(0;5)} f(x) = f(1) = 2\) và hàm số không tồn tại giá trị lớn nhất trên khoảng (0;5)
c) Xét \(h(x) = x\sqrt {2 - {x^2}} \)
Tập xác định: \(D = [ - \sqrt 2 ;\sqrt 2 ]\)
\(h'(x) = \sqrt {2 - {x^2}} - \frac{{{x^2}}}{{\sqrt {2 - {x^2}} }}\)
Tập xác định mới: \({D_1} = ( - \sqrt 2 ;\sqrt 2 )\)
\(h'(x) = 0 \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = - 1\end{array} \right.\)
Bảng biến thiên:
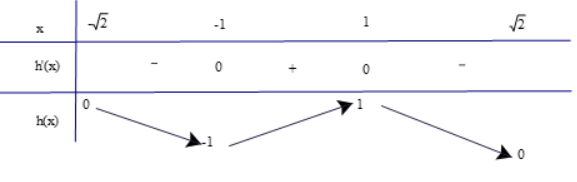
Từ bảng biến thiên, ta thấy \(\mathop {\min }\limits_D f(x) = f( - 1) = - 1\) và \(\mathop {\max }\limits_D f(x) = f(1) = 1\)


