Question

Sử dụng ý nghĩa hình học của tích phân, tính:

a) \(\int\limits^2_1\left(2x+1\right)dx;\)                     b) \(\int\limits^3_{-3}\left(\sqrt{9-x^2}\right)dx.\)

Answer 1

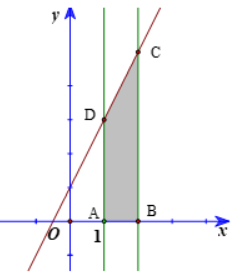
a) Tích phân cần tính là diện tích của hình thang vuông ABCD, có đáy nhỏ \(AB = 3,\) đáy lớn \(CD = 5\) và đường cao \(AD = 1\).

Do đó, \(\int\limits_1^2 {\left( {2x + 1} \right)dx}  = {S_{ABCD}} = \frac{1}{2}\left( {AB + CD} \right)AD = \frac{1}{2}\left( {3 + 5} \right).1 = 4\)

b) Ta có \(y = \sqrt {9 - {x^2}} \) là phương trình nửa phía trên trục hoành của đường tròn tâm tại gốc tọa độ O và bán kính 3. Do đó, tích phân cần tính là diện tích nửa phía trên trục hoành của hình tròn tương ứng.

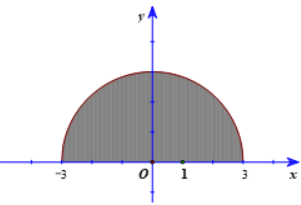
Vậy \(\int\limits_{ - 3}^3 {\sqrt {9 - {x^2}} dx}  = \frac{9}{2}\pi \)