Sử dụng một hình cầu bán kính R và một cốc thủy tinh có dạng hình trụ bán kính đáy R, chiều cao 2R. Ban đầu để hình cầu nằm khít trong chiếc cốc có đầy nước.
Ta nhấc hình cầu ra khỏi cốc thủy tinh hình trụ (H.10.25).
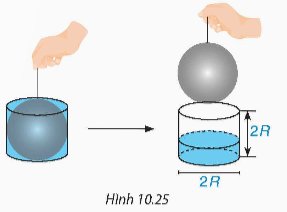
Đo độ cao cột nước còn lại trong chiếc cốc, ta thấy độ cao này chỉ bằng \(\dfrac{1}{3}\) chiều cao của chiếc cốc hình trụ. Từ đó, em hãy dự đoán công thức tính thể tích hình cầu bán kính R.
Thể tích của nước trong cốc khi hình cầu trong cốc:
\({V_1} = \pi {R^2}.2R = 2\pi {R^3}\).
Thể tích của nước trong cốc khi bỏ hình cầu ra ngoài:
\({V_2} = \pi {R^2}.\frac{1}{3}.2R = \frac{2}{3}\pi {R^3}\).
Thể tích của hình cầu là:
\(V = {V_1} - {V_2} = 2\pi {R^3} - \frac{2}{3}\pi {R^3} = \frac{4}{3}\pi {R^3}\).
Dự đoán công thức tính thể tích hình cầu bán kính R:
\(V = \frac{4}{3}\pi {R^3}\).


