Xét \(y(t) = 5 - \frac{{15t}}{{9{t^2} + 1}}\) trên nửa đoạn \([0; + \infty )\)
\(y'(t) = \frac{{135{t^2} - 15}}{{{{(9{t^2} + 1)}^2}}} = 0 \Leftrightarrow \left[ \begin{array}{l}x = \frac{1}{3}\\x = - \frac{1}{3}(loai)\end{array} \right.\)
Bảng biến thiên:
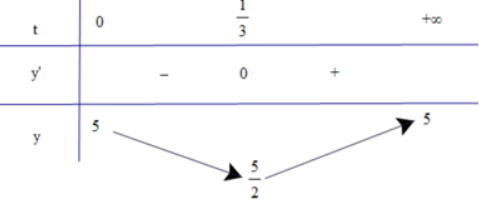
Từ bảng biến thiên, ta thấy \(\mathop {\min }\limits_{[0; + \infty )} y(t) = y(\frac{1}{3}) = - \frac{5}{2}\) và \(\mathop {\max }\limits_{[0; + \infty )} y(t) = y(0) = 5\)
Vậy vào các thời điểm t = 0 thì nồng độ oxygen trong nước cao nhất và t = \(\frac{1}{3}\) giờ thì nồng độ oxygen trong nước thấp nhất
Đúng 0
Bình luận (0)


