\(A=\left(a+b\right)^5-a^5-b^5\)
\(A=a^5+5a^4b+10a^3b^2+10a^2b^3+5ab^4+a^5-a^5-b^5\)
\(A=5a^4b+5ab^4+10a^3b^2+10a^2b^3\)
\(A=5ab\left(a^3+b^3\right)+10a^2b^2\left(a+b\right)\)
\(A=5ab\left(\left(a+b\right)^3-3ab\left(a+b\right)\right)+10a^2b^2\left(a+b\right)\)
\(A=5ab\left(a+b\right)^3-15a^2b^2\left(a+b\right)+10a^2b^2\left(a+b\right)\)
\(A=5ab\left(a+b\right)^3-5a^2b^2\left(a+b\right)\)
\(A=5ab\left(a+b\right)\left(\left(a+b\right)^2-ab\right)\)
\(A=5ab\left(a+b\right)\left(a^2+2ab+b^2-ab\right)\)
\(A=5ab\left(a+b\right)\left(a^2+ab+b^2\right)\)
A= (x+y)5 - x5 - y5 = (x5 + 5x4y + 10x3y2 + 10x2y3 + 5xy4 + y5) - x5 y5
= 5x4y + 10x3y2 + 10x2y3 + 5xy4 = 5xy(x3 + 2x2y + 2xy2 + y3)
= 5xy[(x+y)(x2 - xy + y2) + 2xy(x+y)] = 5xy(x+y)(x2 + xy + y2)
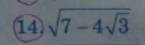phân tích thành nhân tử
phân tích đa thức thành nhân tử
phân tích đa thức thành nhân tử ạ
