Tham khảo
Bước 1:
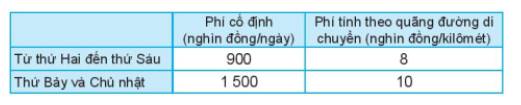
Gọi x là số phút gọi nội mạng (\(x \in \mathbb{N}\)), y là số phút gọi ngoại mạng (\(y \in \mathbb{N}\))
Số tiền cần phải trả là \(x + 2y\) nghìn đồng.
Để số tiền phải trả ít hơn 200 nghìn đồng thì \(x + 2y < 200\).
Như vậy, bài toán trở thành tìm miền nghiệm của bất phương trình \(x + 2y < 200\)
Bước 2:
Xác định miền nghiệm:
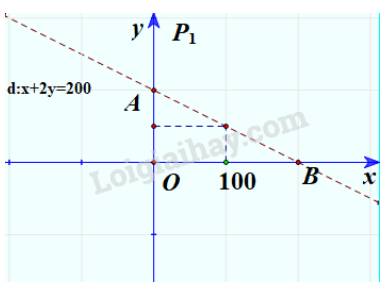
+ Vẽ đường thẳng d: x+2y=200 (nét đứt).
+ Thay tọa độ O(0;0) vào biểu thức x+2y ta được 0+2.0=0<200
=> Miền nghiệm của bất phương trình là nửa mặt phẳng bờ d chứa gốc tọa độ không kể đường thẳng d.
Vậy nếu số phút sử dụng nội mạng là x và ngoại mạng là y mà điểm (x;y) nằm trong miền tam giác OAB không kể đoạn AB thì số tiền phải trả thấp hơn 200 nghìn đồng.
Chú ý
x và y là số tự nhiên nên cần lấy phần không âm của trục Ox và phần không âm của trục Oy.