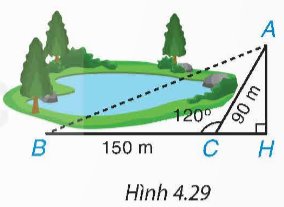
Ta có: \(\widehat {BCA} + \widehat {ACH} = {180^0}\) (kề bù) suy ra \(\widehat {ACH} = 180^\circ - \widehat {BCA} = 180^\circ - 120^\circ = 60^\circ\)
Nên \(AH = AC.\sin \widehat {ACH} = 90.\sin 60 = 45\sqrt 3 \) m
\(CH = AC.\cos \widehat {ACH} = 90.\cos {60^0} = 45\) m
Do đó \(BH = BC + CH = 150 + 45 = 195\) m
Tam giác ABH vuông tại H nên \(A{B^2} = A{H^2} + B{H^2}\) (định lý Pythagore)
Thay số ta có \(A{B^2} = {\left( {45\sqrt 3 } \right)^2} + {195^2}= 44100\) hay \(AB = 210\) m.
Đúng 0
Bình luận (0)