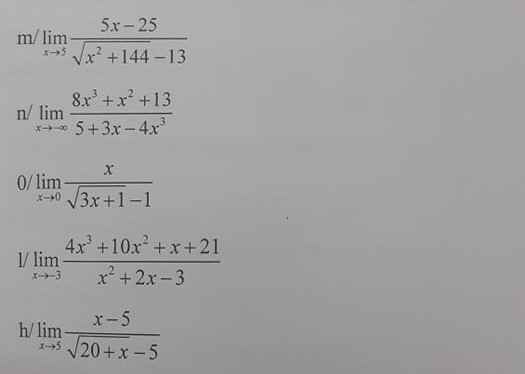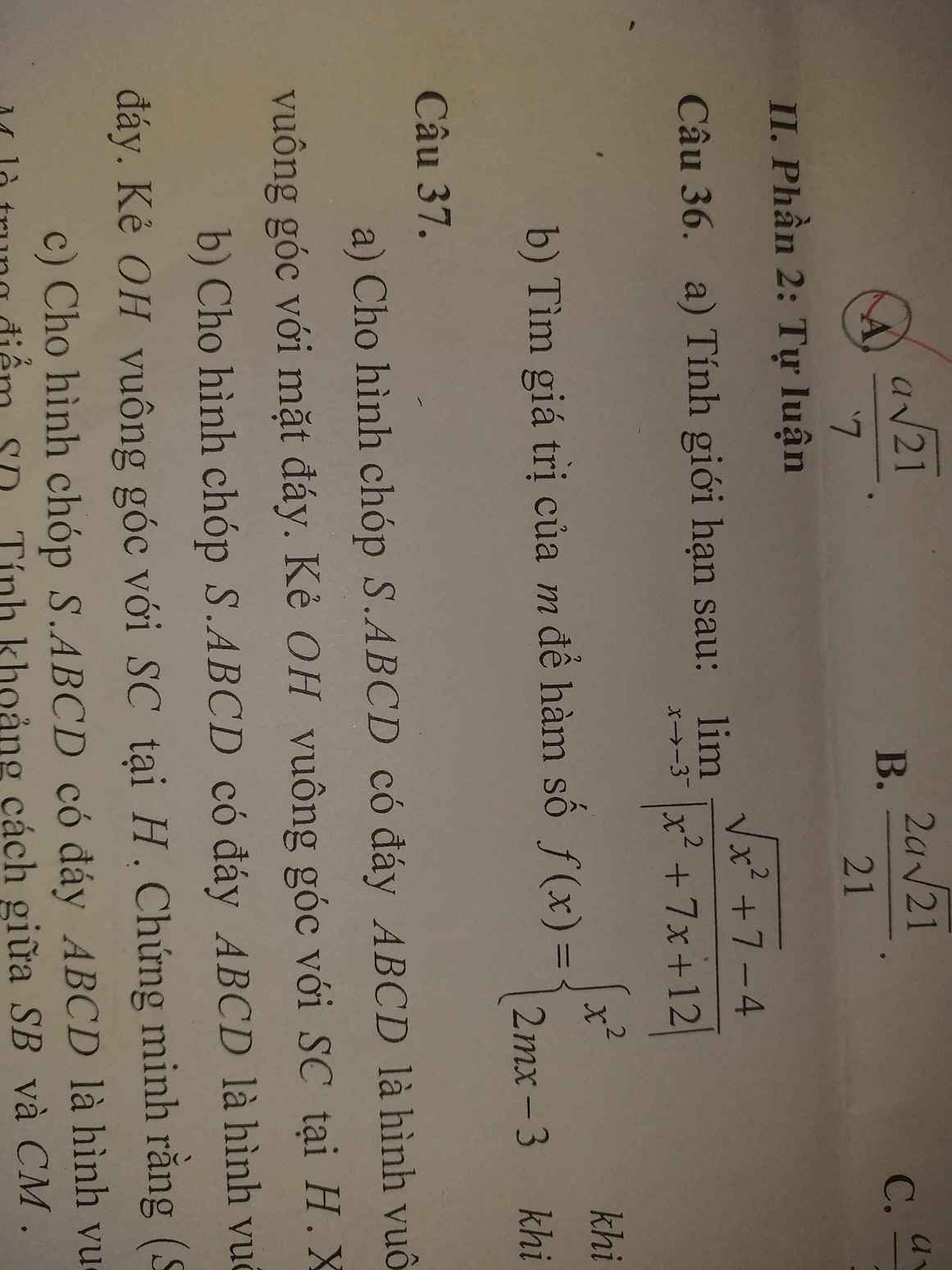Lời giải:
m.
\(\lim\limits_{x\to 5}\frac{5x-25}{\sqrt{x^2+144}-13}=\lim\limits_{x\to 5}\frac{5(x-5)}{\frac{x^2-25}{\sqrt{x^2+144}+13}}=\lim\limits_{x\to 5}\frac{5(\sqrt{x^2+144}+13)}{x+5}=13\)
n.
\(\lim\limits_{x\to -\infty}\frac{8x^3+x^2+13}{5+3x-4x^3}=\lim\limits_{x\to -\infty}\frac{8+\frac{1}{x}+\frac{13}{x^3}}{\frac{5}{x^3}+\frac{3}{x^2}-4}=\frac{8}{-4}=-2\)
0.
\(\lim\limits_{x\to 0}\frac{x}{\sqrt{3x+1}-1}=\lim\limits_{x\to 0}\frac{x}{\frac{3x}{\sqrt{3x+1}+1}}=\lim\limits_{x\to 0}\frac{\sqrt{3x+1}}{3}=\frac{1}{3}\)
l.
\(\lim\limits_{x\to -3}\frac{4x^3+10x^2+x+21}{x^2+2x-3}=\lim\limits_{x\to -3}\frac{(x+3)(4x^2-2x+7)}{(x+3)(x-1)}=\lim\limits_{x\to -3}\frac{4x^2-2x+7}{x-1}=\frac{-49}{4}\)
h.
\(\lim\limits_{x\to 5}\frac{x-5}{\sqrt{x+20}-5}=\lim\limits_{x\to 5}\frac{x-5}{\frac{x-5}{\sqrt{20+x}+5}}=\lim\limits_{x\to 5}(\sqrt{20+x}+5)=10\)
P/s: Mẫu chốt của các bài toán này là bạn khi $x\to a$ thì bạn cố gắng làm triệt tiêu nhân tố $x-a$ ở các hàm số.