Question

Khi làm nhà kho, bác An muốn cửa số có dạng hình chữ nhật với chu vi bằng 4 m (Hình 6). Tìm kích thước khung cửa sổ sao cho diện tích cửa sổ lớn nhất (để hứng được nhiều ánh sáng nhất)?

Answer 1

Gọi a, b lần lượt là chiều dài và chiều rộng của cửa sổ (m; a,b > 0)

Chu vi cửa sổ là: \(2(a + b) = 4 \Leftrightarrow b = 2 - a\)

Diện tích cửa sổ là: \(y = ab = a(2 - a) =  - {a^2} + 2a\)

\(y' =  - 2a + 2 = 0 \Leftrightarrow a = 1\)

Bảng biến thiên:

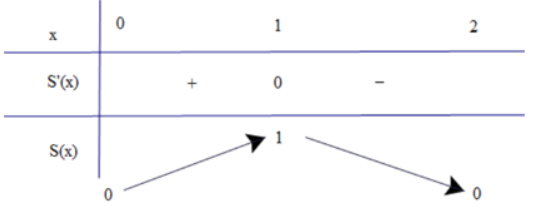
Từ bảng biến thiên, ta thấy \(\mathop {\max }\limits_{(0; + \infty )} y = y(1) = 1\)

Vậy để diện tích cửa sổ lớn nhất bằng \(1{m^2}\) thì chiều dài và chiều rộng bằng nhau và bằng 1m