a,
\(y = 2{x^3} - 3{x^2} + 1\)
Tập xác định: D = R
\(y' = 6{x^2}\) - 6x; y' = 0 \( \Rightarrow \left[ {\begin{array}{*{20}{c}}{x = 1}\\{x = 0}\end{array}} \right.\)
Bảng biến thiên
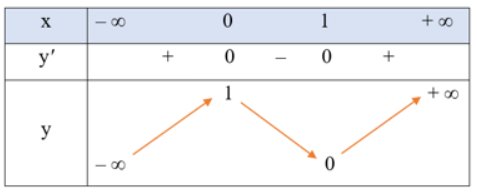
Đồ thị hàm số
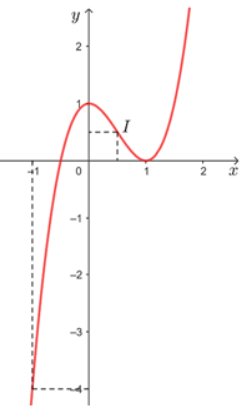
b,
\(y = - {x^3} + 3{x^2} - 1\)
Tập xác định: D = R
\(y' = - 3{x^2} + 6x\); y' = 0 \( \Rightarrow \left[ {\begin{array}{*{20}{c}}{x = 0}\\{x = 2}\end{array}} \right.\)
Bảng biến thiên
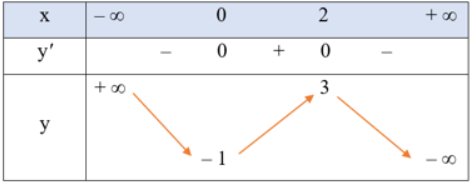
Đồ thị hàm số
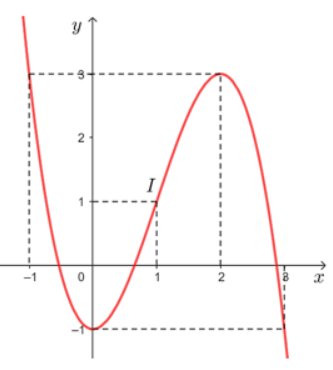
c,
\(y = {\left( {x - 2} \right)^3} + 4\)
Tập xác định: D = R
\(y' = 3{\left( {x - 2} \right)^2} \), y’=0 \( = > {\left( {x\;-\;2} \right)^2} = 0 = > x - 2 = 0 = > x = 2\)
Bảng biến thiên
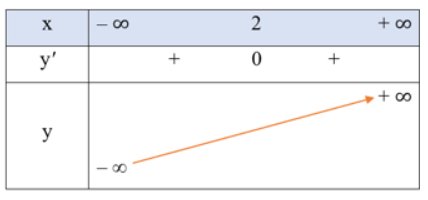
Đồ thị hàm số
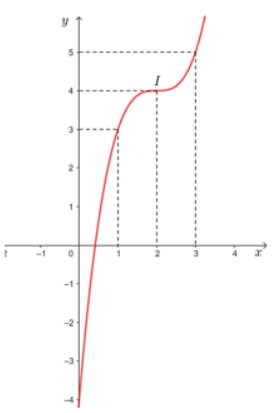
d,
\(y = - {x^3} + 3{x^2} - 3x + 2\)
Tập xác định: D = R
\(y' = - 3{x^2} + 6x - 3,\;y' = 0 = > x = 1\)
Bảng biến thiên:
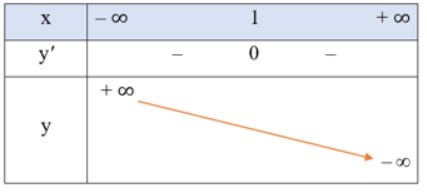
Đồ thị hàm số
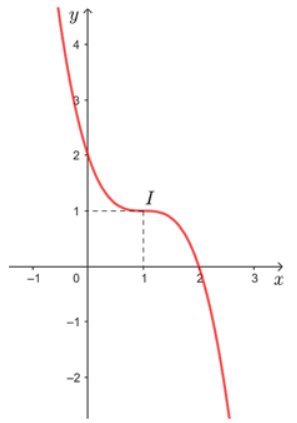
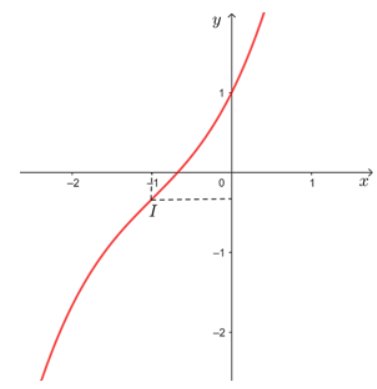
e,\(y = \frac{1}{3}{x^3} + {x^2} + 2x + 1 = > y' = {x^2} + 2x + 2 > 0, \forall x \in D\)
Tập xác định: D = R
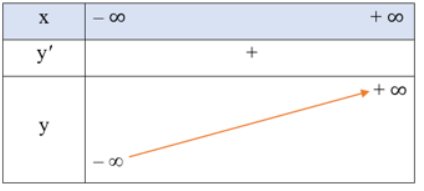
Đồ thị hàm số
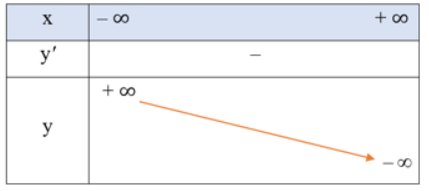
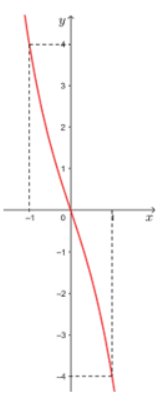
g,\(y = - {x^3} - 3x = > y' = - 3{x^2} - 3 < 0, \forall x \in D\)
Tập xác định: D = R
Bảng biến thiên
Đồ thị hàm số
\( \Rightarrow \left[ {\begin{array}{*{20}{c}}{x = 1}\\{x = 0}\end{array}} \right.\)


