Question

Hộp sữa 1 l được thiết kế dạng hình hộp chữ nhật với đáy là hình vuông cạnh x cm. Tìm x để diện tích toàn phần của hộp nhỏ nhất.

Answer 1

Gọi chiều cao của hộp là h (cm)

Thể tích của hộp là: \(V = h.{x^2} = 1 \Leftrightarrow h = \frac{1}{{{x^2}}}\)

Diện tích toàn phần của hộp là: \(y = {S_{tp}} = {S_{xq}} + {S_{day}} = 4hx + 2{x^2} = 4.\frac{1}{{{x^2}}}.x + 2{x^2} = 2{x^2} + \frac{4}{x}\)

Tập xác định: \(D = (0; + \infty )\)

\(y' = 4x - \frac{4}{{{x^2}}} = 0 \Leftrightarrow x = 1\)

Bảng biến thiên:

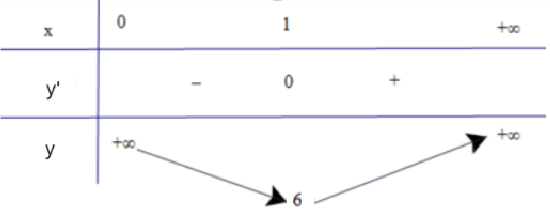
Từ bảng biến thiên, ta thấy \(\mathop {\min }\limits_D y = y(1) = 6\)

Vậy x = 1 cm thì diện tích toàn phần của hộp nhỏ nhất và bằng 6 \(c{m^2}\)