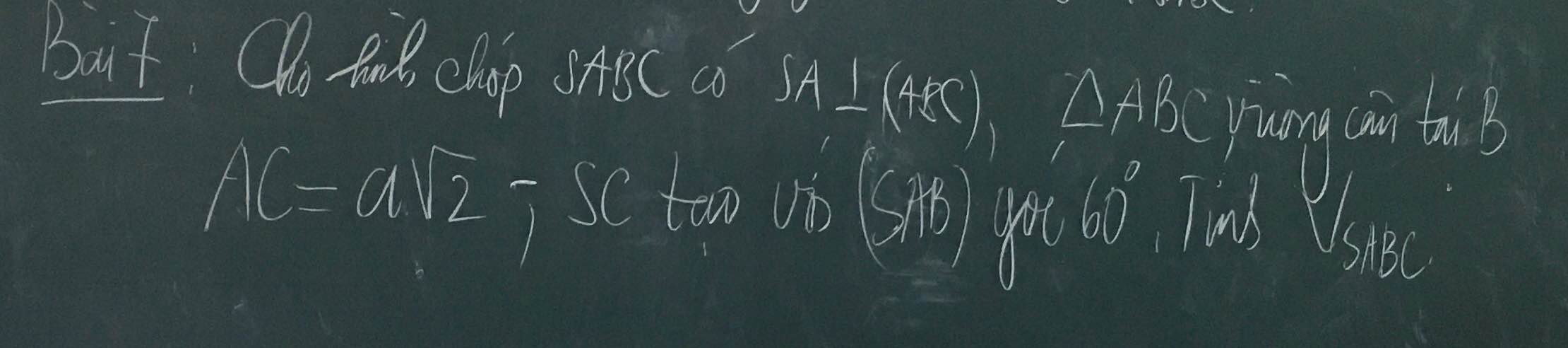Ta có :
$SA ⊥ BC$ ; $AB ⊥ BC$ suy ra $BC ⊥ (SAB)$
Do đó $(SC;(SAB)) = ∠BSC = 60^o$
Tam giác ABC vuông cân tại B nên ta có :
$BA^2 + BC^2 = AC^2 = 2a^2 \Rightarrow BA = BC = a$
Ta có : $SC.sin(BSC) = BC \Rightarrow SC = \dfrac{a}{sin(60^o)}$ = \(\dfrac{2\sqrt{3}}{3}\)a
$SA^2 + AC^2 = SC^2 \Rightarrow SA = $\(\dfrac{\sqrt{3}}{3}\)a
Vậy, \(V_{S.ABC}=\dfrac{1}{3}.\dfrac{\sqrt{3}}{3}a.\dfrac{1}{2}.a.a=\dfrac{\sqrt{3}}{18}a^3\)
Đúng 1
Bình luận (0)
