Hình 3 cho ta đồ thị của ba hàm số
\(y=f\left(x\right)=\dfrac{1}{2}x^2;y=g\left(x\right)=\left\{{}\begin{matrix}\dfrac{1}{2}x^2\text{ nếu x}\le2\\-4x+10\text{ nếu }x\ge2\end{matrix}\right.\) và \(y=h\left(x\right)=3-\dfrac{1}{2}x^2\) trên đoạn [-1; 3].
a) Hàm số nào đạt giá trị lớn nhất tại một điểm cực đại của nó?
b) Các hàm số còn lại đạt giá trị lớn nhất tại điểm nào?
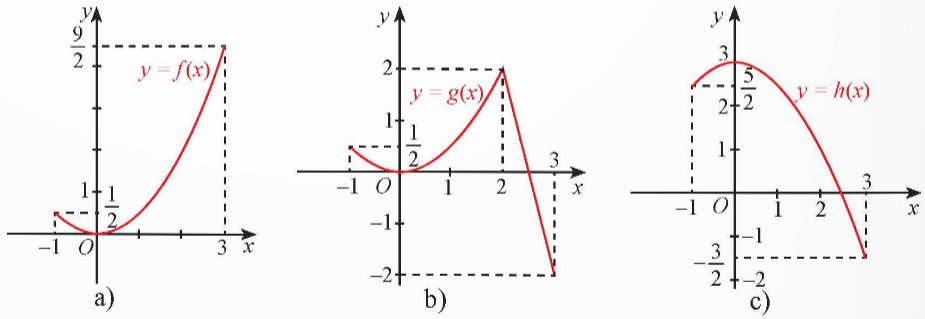
a) \(h(x)\)đạt giá trị cực đại tại x = 0 và \(\mathop {\max h(x)}\limits_{[ - 1;3]} = h(0) = 3\)
b) \(\mathop {\max f(x)}\limits_{[ - 1;3]} = f(3) = \frac{9}{2}\) và \(\mathop {\max g(x)}\limits_{[ - 1;3]} = g(2) = 2\)
Đúng 0
Bình luận (0)


