Question

Hai lò xo có độ cứng k = 250 N/m, l0 = 36cm. Hai vật có khối lượng m kích thước nhỏ có thể trượt không ma sát trên trục nằm ngang. Quay hệ quanh trục thẳng đứng với tần số n = 2 vòng/s. Cho m = 200 g. Tính chiều dài mỗi lò xo.

Answer 1

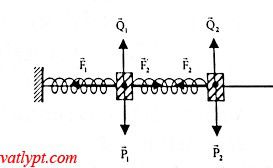
Vật 1 : \(\overrightarrow{P_1}+\overrightarrow{Q_1}+\overrightarrow{F_1}+\overrightarrow{F_1'}=m\overrightarrow{a}_1\)

=> F1 - F'2 = ma= \(m\omega\left(l_0+\Delta l_1\right)\left(1\right)\)

Vật 2 : \(\overrightarrow{P_2}+\overrightarrow{Q_2}+\overrightarrow{F_2}=m\overrightarrow{a_1}\)

=> F2 = \(m\omega^2\left(2l_0+\Delta l_1+\Delta l_2\right)\left(2\right)\)

Ta có: F2 = F'2=\(k\Delta l_{2;}F_1=k\Delta l_1;\omega=2\pi n\); thay vào (1); (2) giải hệ => \(\left\{{}\begin{matrix}\Delta l_1=21cm\\\Delta l_2=14cm\end{matrix}\right.\)

=> l1 =57cm; l2 = 50cm.