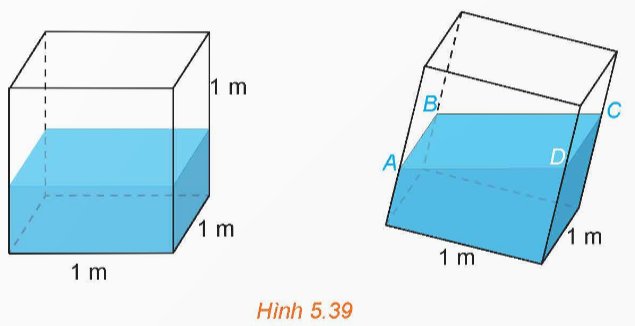
(H.5.39) Trong một bể hình lập phương cạnh 1 m có chứa một ít nước. Người ta đặt đáy bể nghiêng so với mặt phẳng nằm ngang. Biết rằng, lúc đó mặt nước có dạng hình bình hành ABCD và khoảng cách từ các điểm A, B, C đến đáy bể tương ứng là 40 cm, 44 cm, 48 cm.
a) Khoảng cách từ điểm D đến đáy bể bằng bao nhiêu centimét? (Tính gần đúng, lấy giá trị nguyên).
b) Đáy bể nghiêng so với mặt phẳng nằm ngang một góc bao nhiêu độ?
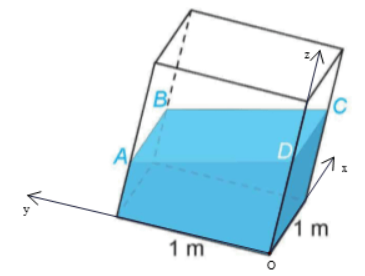
a) Chọn hệ trục tọa độ Oxyz như hình vẽ.
Khi đó, \(A\left( {0;1;0,4} \right),B\left( {1;1;0,44} \right),C\left( {1;0;0,48} \right),D\left( {0;0;z} \right)\)
Suy ra: \(\overrightarrow {AB} \left( {1;0;0,04} \right),\overrightarrow {DC} \left( {1;0,0,48 - z} \right)\)
Vì ABCD là hình bình hành nên \(\overrightarrow {AB} = \overrightarrow {DC} \Rightarrow 0,48 - z = 0,04 \Rightarrow z = 0,44\)
Do đó, \(D\left( {0;0;0,44} \right)\). Vậy khoảng cách từ D đến đáy bể bằng 44cm.
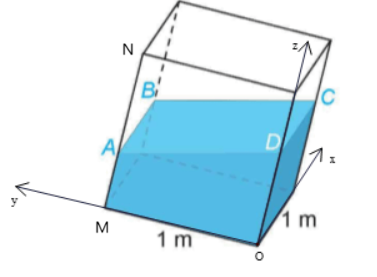
b) Đặt tên các điểm như hình vẽ. Kẻ AA’ vuông góc với Oz tại A’.
Mặt phẳng (Oxz) nhận \(\overrightarrow j \left( {0;1;0} \right)\) làm vectơ pháp tuyến nên phương trình mặt phẳng (Oxz) là: \(y = 0\).
Ta có: \(AA' = d\left( {A,\left( {Oxz} \right)} \right) = \frac{{\left| 1 \right|}}{{\sqrt 1 }} = 1\), \(AD = \sqrt {{1^2} + 0,{{04}^2}} = \frac{{\sqrt {626} }}{{25}}\)
Tam giác ADA’ vuông tại A’ nên \(\cos \left( {AA',DA} \right) = \frac{{AA'}}{{AD}} = \frac{1}{{\frac{{\sqrt {626} }}{{25}}}} \Rightarrow \left( {AA',AD} \right) \approx 2,{3^o}\)
Vậy đáy bể nghiêng mới mặt nằm ngang một góc khoảng \(2,{3^o}\).


