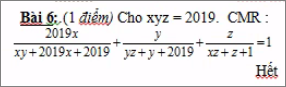Câu 5:
\(\text{a) }A=\dfrac{5x+1}{x^3-1}-\dfrac{1-2x}{x^2+x+1}-\dfrac{2}{1-x}\\ A=\dfrac{5x+1}{x^3-1}-\dfrac{1-2x}{x^2+x+1}+\dfrac{2}{x-1}\\ A=\dfrac{5x+1}{\left(x^2+x+1\right)\left(x-1\right)}-\dfrac{\left(1-2x\right)\left(x-1\right)}{\left(x^2+x+1\right)\left(x-1\right)}+\dfrac{2\left(x^2+x+1\right)}{\left(x-1\right)\left(x^2+x+1\right)}\\ A=\dfrac{5x+1-\left(1-2x\right)\left(x-1\right)+2\left(x^2+x+1\right)}{\left(x-1\right)\left(x^2+x+1\right)}\\ \)
\(\Rightarrow\) Để \(A\) được xác định
\(\text{thì }\Rightarrow\left(x-1\right)\left(x^2+x+1\right)\ne0\\ \Leftrightarrow x-1\ne0\\ \Leftrightarrow x\ne1\)
\(\text{b) }A=\dfrac{5x+1-\left(1-2x\right)\left(x-1\right)+2\left(x^2+x+1\right)}{\left(x-1\right)\left(x^2+x+1\right)}\\ A=\dfrac{5x+1-\left(x-1\right)+2x\left(x-1\right)+2x^2+2x+2}{\left(x-1\right)\left(x^2+x+1\right)}\\ A=\dfrac{5x+1-x+1+2x^2-2x+2x^2+2x+2}{\left(x-1\right)\left(x^2+x+1\right)}\\ A=\dfrac{4x+4+4x^2}{\left(x-1\right)\left(x^2+x+1\right)}\\ A=\dfrac{4\left(x+1+x^2\right)}{\left(x-1\right)\left(x^2+x+1\right)}\\ A=\dfrac{4}{x-1}\)
c) Để \(A>0\)
\(\text{thì }\Rightarrow\dfrac{4}{x-1}>0\\ \text{Mà }4>0\\ \Leftrightarrow x-1>0\\ \Leftrightarrow x>1\)
Vậy........................