10.
\(x^3+8+\left(x+2\right)\left(x+4\right)=\left(x+2\right)\left(x^2-2x+4\right)+\left(x+2\right)\left(x+4\right)\)
\(=\left(x+2\right)\left(x^2-x+8\right)\)
11.
\(2x\left(3x-5\right)-10+6x=2x\left(3x-5\right)+2\left(3x-5\right)=2\left(x+1\right)\left(3x-5\right)\)
12.
\(\left(5x-4\right)^2-\left(7x\right)^2=\left(5x-4-7x\right)\left(5x-4+7x\right)=\left(-2x-4\right)\left(12x-4\right)=-8\left(x+2\right)\left(3x-1\right)\)
13.
\(4x^2+4x+1-9y^2=\left(2x+1\right)^2-\left(3y\right)^2=\left(2x+1-3y\right)\left(2x+1+3y\right)\)
14.
\(x^2-2xy+y^2+4x-4y=\left(x-y\right)^2+4\left(x-y\right)=\left(x-y\right)\left(x-y+4\right)\)
10)
\(x^3+8-\left(x+2\right)\left(x+4\right)\\ =\left(x+2\right)\left(x^2-2x+4\right)-\left(x+2\right)\left(x+4\right)\\ =\left(x+2\right)\left[\left(x^2-2x+4\right)-\left(x+4\right)\right]\\ =\left(x+2\right)\left(x^2-2x+4-x-4\right)\\ =\left(x+2\right)\left(x^2-3x\right)\\ =x\left(x+2\right)\left(x-3\right)\)
11)
\(2x\left(3x-5\right)-10+6x\\ =6x^2-10x-10+6x\\ =6x^2-4x+10\\ =2\left(3x^2-2x+5\right)\)
12)
\(\left(5x-4\right)^2-49x^2\\ =\left[\left(5x-4\right)-7x\right]\left[\left(5x-4\right)+7x\right]\\ =\left(-4-2x\right)\left(13x-4\right)\\ =\left[-2\left(2+x\right)\right]\left(13x-4\right)\)
14)
\(x^2+4x-2xy-4y+y^2\\ =\left(4x-4y\right)+\left(x^2-2xy+y^2\right)\\ =4\left(x-y\right)+\left(x-y\right)^2\\ =\left(x-y\right)+\left[4\left(x-y\right)\right]\)
13)
\(4x^2+4x-9y^2+1\\ =4x\left(x+1\right)-9y^2+1\)

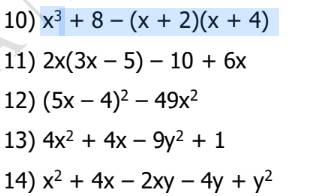














 iupspui
iupspui