Câu 2:
a) Vì (d) cắt trục tung tại điểm có tung độ bằng 3:
\(\Rightarrow3=\left(m+2\right).0+2m^2+1\)
\(\Leftrightarrow m^2=1\)
\(\Leftrightarrow m=\pm1\) (nhận)
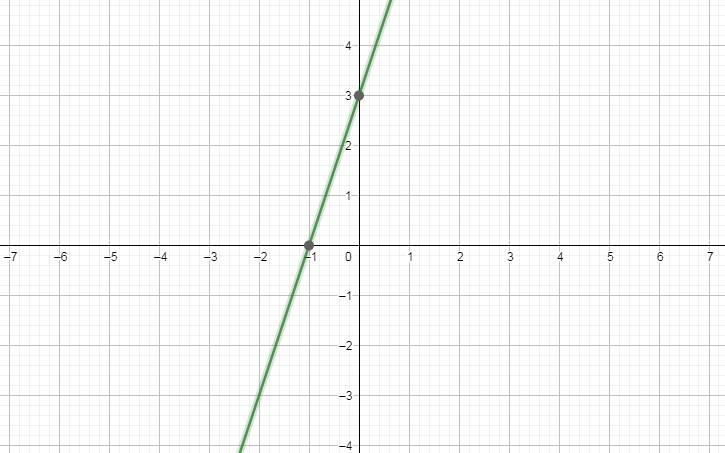
Với \(m=1\Rightarrow y=\left(1+2\right)x+2.1^2+1\Rightarrow y=3x+3\).
Bảng giá trị:
x -1 0
\(y=3x+3\) 0 3
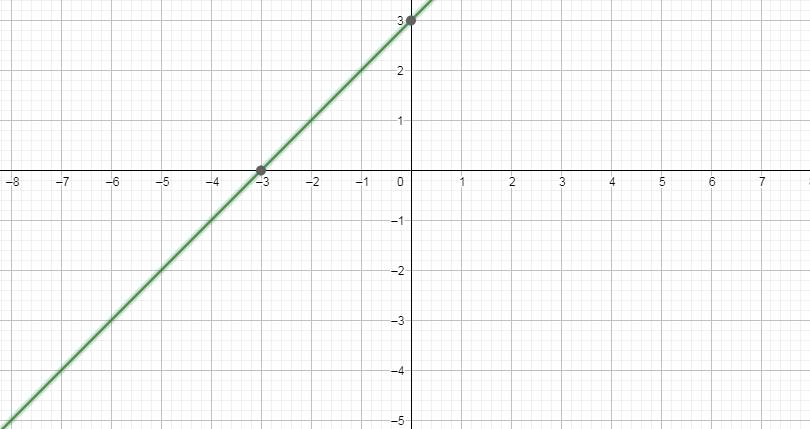
Với \(m=-1\Rightarrow y=\left(-1+2\right)x+2.\left(-1\right)^2+1=x+3\)
Bảng giá trị:
x -3 0
\(y=x+3\) 0 3
Câu 2:
b) Gọi \(A\left(x_0;y_0\right)\) là tọa độ giao điểm của (d) và (d'). Vì A nằm trên trục tung Oy \(\Rightarrow A\left(0;y_0\right)\).
- Thay \(A\left(0;y_0\right)\) vào pt \(\left(d\right):y=\left(m+2\right)x+2m^2+1\) ta được:
\(y_0=\left(m+2\right).0+2m^2+1\Rightarrow y_0=2m^2+1\left(1\right)\)
- Thay \(A\left(0;y_0\right)\) vào pt \(\left(d'\right):y=\left(2m+2\right)x-m+1\)
\(y_0=\left(2m+2\right).0-m+1\Rightarrow y_0=-m+1\left(2\right)\)
Từ (1), (2) ta có: \(2m^2+1=-m+1\)
\(\Leftrightarrow2m^2+m=0\)
\(\Leftrightarrow m\left(2m+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}m=0\\m=-\dfrac{1}{2}\end{matrix}\right.\)
c) Gọi B là giao của (d) và trục hoành Ox \(\Rightarrow B\left(x_1;0\right)\) (x1 là số nguyên).
Thay \(B\left(x_1;0\right)\) vào pt \(\left(d\right):y=\left(m+2\right)x+2m^2+1\) ta được:
\(0=\left(m+2\right)x_1+2m^2+1\)
\(\Rightarrow x_1=-\dfrac{2m^2+1}{m+2}=-\dfrac{2\left(m^2-4\right)+9}{m+2}=-\dfrac{2\left(m-2\right)\left(m+2\right)+9}{m+2}=-2\left(m-2\right)-\dfrac{9}{m+2}\)Để x1 là số nguyên thì \(9⋮\left(m+2\right)\)
\(\Rightarrow m+2\inƯ\left(9\right)\)
\(\Rightarrow m+2\in\left\{1;-1;9;-9\right\}\)
\(\Rightarrow m\in\left\{-1;-3;7;-11\right\}\)






















