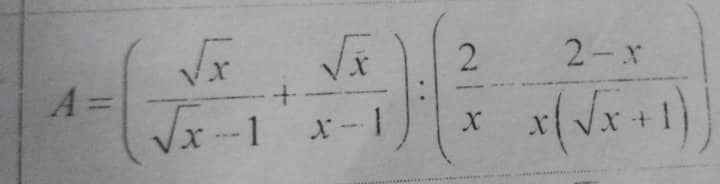đk x > 0 ; x≠1
\(A=\left(\dfrac{\sqrt{x}\left(\sqrt{x}+1\right)+\sqrt{x}}{x-1}\right):\left(\dfrac{2\left(\sqrt{x}+1\right)-2+x}{x\left(\sqrt{x}+1\right)}\right)\\ =\left(\dfrac{x+\sqrt{x}+\sqrt{x}}{x-1}\right):\left(\dfrac{2\sqrt{x}+2-2+x}{x\left(\sqrt{x}+1\right)}\right)\\ =\dfrac{x+2\sqrt{x}}{x-1}.\dfrac{x\left(\sqrt{x}+1\right)}{x+2\sqrt{x}}\\ =\dfrac{x}{\sqrt{x}-1}\)
\(A=\left(\dfrac{\sqrt{x}}{\sqrt{x}-1}+\dfrac{\sqrt{x}}{x-1}\right):\left(\dfrac{2}{x}-\dfrac{2-x}{x\left(\sqrt{x}+1\right)}\right)\left(x>0;x\ne1\right)\\ =\dfrac{\sqrt{x}\left(\sqrt{x}+1\right)+\sqrt{x}}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}:\dfrac{2\left(\sqrt{x}+1\right)-\left(2-x\right)}{x\left(\sqrt{x}+1\right)}\\ =\dfrac{x+\sqrt{x}+\sqrt{x}}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}.\dfrac{x\left(\sqrt{x}+1\right)}{2\sqrt{x}+2-2+x}\\ =\dfrac{x+2\sqrt{x}}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}.\dfrac{x\left(\sqrt{x}+1\right)}{x+2\sqrt{x}}\\ =\dfrac{x}{\sqrt{x}-1}\)