Giải quyết bài toán ở tình huống mở đầu.
Một cây cầu treo có trụ tháp đôi cao 75 m so với mặt của cây cầu và cách nhau 400 m. Các dây cáp có dạng đồ thị của hàm số y = ax2 (a ≠ 0) như Hình 6.1 và được treo trên các đỉnh tháp. Tìm chiều cao CH của dây cáp biết điểm H cách tâm O của cây cầu 100 m (giả sử mặt của cây cầu là bằng phẳng).
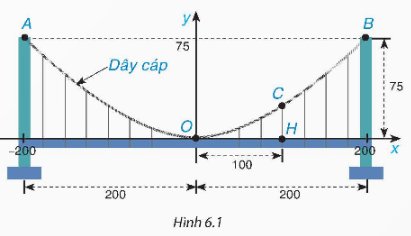
Đồ thị hàm số \(y = a{x^2}\) đi qua điểm (200; 75) nên ta có: \(75 = a{.200^2} \Rightarrow a = \frac{3}{{1600}}\).
Khi đó, \(y = \frac{3}{{1600}}{x^2}\).
Với \(x = 100\) ta có: \(y = \frac{3}{{1600}}{.100^2} = \frac{{75}}{4}\).
Vậy chiều cao \(CH = \frac{{75}}{4}m\) khi điểm H cách tâm O của cây cầu 100m.