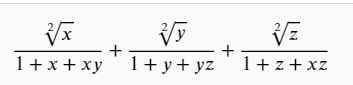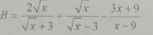1.
a)\(A=\sqrt{3}\left(2\sqrt{27}-6\sqrt{\dfrac{1}{3}}+\dfrac{3}{2}\sqrt{12}\right)\)
\(\Leftrightarrow A=\sqrt{3}\left(6\sqrt{3}-2\sqrt{3}+3\sqrt{3}\right)=\sqrt{3}\cdot7\sqrt{3}\)
\(\Leftrightarrow A=21\)
\(B=\dfrac{x+\sqrt{x}}{\sqrt{x}}+\dfrac{x-4}{\sqrt{x}+2}\left(x>0\right)\\ \Leftrightarrow B=\dfrac{\sqrt{x}\left(\sqrt{x}+1\right)}{\sqrt{x}}+\dfrac{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}{\sqrt{x}+2}\\ \Leftrightarrow B=\sqrt{x}+1+\sqrt{x}-2=2\sqrt{x}-1\)
b) Để \(A=B\)
\(\Leftrightarrow2\sqrt{x}-1=21\\ \Leftrightarrow2\sqrt{x}=22\\ \Leftrightarrow\sqrt{x}=11\\ \Leftrightarrow x=121\)
3.
a)\(A=\left(\sqrt{5}-\sqrt{2}\right)^2+\sqrt{40}\)
\(\Leftrightarrow A=7-2\sqrt{10}+2\sqrt{10}\\ \Leftrightarrow A=7\)
\(B=\left(\dfrac{x-\sqrt{x}}{\sqrt{x}-1}-\dfrac{\sqrt{x}+1}{x+\sqrt{x}}\right):\dfrac{\sqrt{x}+1}{\sqrt{x}}\left(x>0;x\ne1\right)\\ \Leftrightarrow B=\left(\dfrac{\sqrt{x}\left(\sqrt{x}-1\right)}{\sqrt{x}-1}-\dfrac{\sqrt{x}+1}{\sqrt{x}\left(\sqrt{x}+1\right)}\right)\cdot\dfrac{\sqrt{x}}{\sqrt{x}+1}\\ \Leftrightarrow B=\left(\sqrt{x}-\dfrac{1}{\sqrt{x}}\right)\cdot\dfrac{\sqrt{x}}{\sqrt{x}+1}\\ \Leftrightarrow B=\dfrac{\sqrt{x}-1}{\sqrt{x}+1}\)
b) Để \(A=B\)
\(\dfrac{\sqrt{x}-1}{\sqrt{x}+1}=7\Leftrightarrow\sqrt{x}-1=7\sqrt{x}+7\\ \Leftrightarrow6\sqrt{x}=-8\\ \Leftrightarrow\sqrt{x}=-\dfrac{4}{3}\\ \Leftrightarrow x=\dfrac{16}{9}\)
4.
a)\(A=\left(2\sqrt{75}-5\sqrt{27}-\sqrt{192}+4\sqrt{48}\right):\sqrt{3}\)
\(\Leftrightarrow A=\left(10\sqrt{3}-15\sqrt{3}-8\sqrt{3}+16\sqrt{3}\right):\sqrt{3}\\ \Leftrightarrow A=10-15-8+16=3\)
\(P=\left(\dfrac{\sqrt{x}}{2+\sqrt{x}}+\dfrac{\sqrt{x}}{2-\sqrt{x}}\right):\dfrac{\sqrt{x}}{2+\sqrt{x}}\left(x>0;x\ne4\right)\\ \Leftrightarrow P=\dfrac{\sqrt{x}\left(2-\sqrt{x}\right)+\sqrt{x}\left(2+\sqrt{x}\right)}{\left(2+\sqrt{x}\right)\left(2-\sqrt{x}\right)}\cdot\dfrac{2+\sqrt{x}}{\sqrt{x}}\\ \Leftrightarrow P=\dfrac{2\sqrt{x}-x+2\sqrt{x}+x}{\sqrt{x}\left(2-\sqrt{x}\right)}=\dfrac{4}{2-\sqrt{x}}\)
b) Để \(A=P\)
\(\Leftrightarrow\dfrac{4}{2-\sqrt{x}}=3\\ \Leftrightarrow6-3\sqrt{x}=4\\ \Leftrightarrow3\sqrt{x}=2\\ \Leftrightarrow\sqrt{x}=\dfrac{2}{3}\\ \Leftrightarrow x=\dfrac{4}{9}\)
5.
a)\(A=\sqrt{8+2\sqrt{15}}+\sqrt{8-2\sqrt{15}}\)
\(\Leftrightarrow A=\sqrt{\left(\sqrt{3}+\sqrt{5}\right)^2}+\sqrt{\left(\sqrt{3}-\sqrt{5}\right)^2}\\ \Leftrightarrow A=\sqrt{3}+\sqrt{5}+\sqrt{3}-\sqrt{5}=2\sqrt{3}\)
\(B=\dfrac{1}{\sqrt{x}+2}+\dfrac{1}{2-\sqrt{x}}\left(x\ge0;x\ne4\right)\\ \Leftrightarrow B=\dfrac{2-\sqrt{x}+\sqrt{x}+2}{4-x}=\dfrac{4}{4-x}\)
b) Để \(A=B\Leftrightarrow\dfrac{4}{4-x}=2\sqrt{3}\)
\(\Leftrightarrow2\sqrt{3}\left(4-x\right)=4\\ \Leftrightarrow8\sqrt{3}-2\sqrt{3}x=4\\ \Leftrightarrow2\sqrt{3}x=8\sqrt{3}-4\\ \Leftrightarrow\sqrt{3}x=4\sqrt{3}-2\\ \Leftrightarrow x=\dfrac{4\sqrt{3}-2}{\sqrt{3}}=\dfrac{12-2\sqrt{3}}{3}\)
Tick nha