Question

Giả sử doanh thu (nghìn đồng) của một cửa hàng bán phở trong một ngày có thể mô hình hoá bằng công thức R(x) = x(220 – 4x) với 30 ≤ x ≤ 50, trong đó x (nghìn đồng) là giá tiền của một bát phở. Nếu muốn doanh thu của cửa hàng đạt 3 triệu đồng thì giá bán của mỗi bát phở phải là bao nhiêu?

Answer 1

Ta có 3 triệu đồng = 3 000 nghìn đồng.

Vì doanh thu của cửa hàng đạt 3 triệu đồng nên R(x) = 3 000.

Thay R(x) = 3 000 vào R(x) = x(220 – 4x), ta được:

3 000 = x(220 – 4x)

3 000 = 220x – 4x2

4x2 – 220x + 3 000 = 0

x2 – 55x + 750 = 0.

Ta có ∆ = (–55)2 – 4.1.750 = 25 > 0 và 

Phương trình trên có hai nghiệm phân biệt là:

 

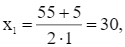
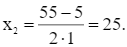
Vì 30 ≤ x ≤ 50 nên ta chọn x = 30 (nghìn đồng).

Vậy nếu muốn doanh thu của cửa hàng đạt 3 triệu đồng thì giá bán của mỗi bát phở là 30 nghìn đồng

 

Answer 2

Để doanh thu cửa hàng đạt 3 triệu đồng thì \(x\left( {220 - 4x} \right) = 3\;000\)

hay \( - {x^2} + 55x - 750 = 0\)

Ta có: \(\Delta  = {55^2} - 4.\left( { - 1} \right).\left( { - 750} \right) = 25 > 0\) nên phương trình có hai nghiệm phân biệt

\({x_1} = \frac{{ - 55 + \sqrt {25} }}{{ - 2}} = 25\left( {KTM} \right);{x_2} = \frac{{ - 55 - \sqrt {25} }}{{ - 2}} = 30\left( {TM} \right)\)

Vậy để doanh thu cửa hàng đạt 3 triệu đồng thì giá bán của mỗi bát phở phải là 30 000 đồng.