Question

Đường cong ở Hình 30 là đồ thị của hàm số:

A. \(y=\dfrac{x^2+2x+2}{-x-1}.\)

B. \(y=\dfrac{x^2+2x+2}{-x-1}.\)

C. \(y=\dfrac{x^2-2x+2}{x-1}\)

D. \(y=\dfrac{x^2-2x+2}{x+1}\)

 

Answer 1

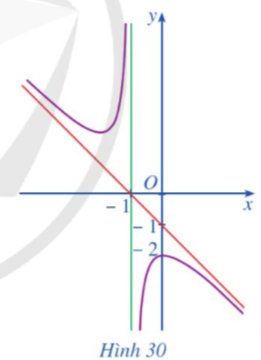
Vì đồ thị hàm số đi qua (0:2)

=> Loại B,D

Vì hàm số có tcd là x=-1

=>\(\mathop {\lim }\limits_{\;x \to  - 1} f\left( x \right) = \infty \)

Xét a,  \(\mathop {\lim }\limits_{x \to  - 1} \frac{{{x^2} + 2x + 2}}{{ - x - 1}} = \mathop {\lim }\limits_{ - x - 1} ( - x - 1 - \frac{1}{{x + 1}}) =  - \infty \)

=> Chọn A