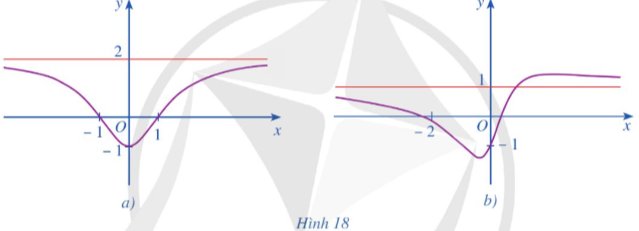
Ta có: \(\mathop {\lim }\limits_{x \to + \infty } y = \mathop {\lim }\limits_{x \to - \infty } y = \frac{{2{x^2} - 2}}{{{x^2} + 2}} = 2\). Do đó đường thẳng \(y = 2\) là một đường tiệm cận ngang của đồ thị hàm số \(y = \frac{{2{x^2} - 2}}{{{x^2} + 2}}\). Vậy đồ thị hàm số \(y = \frac{{2{x^2} - 2}}{{{x^2} + 2}}\) là hình 18a.
Tương tự, \(\mathop {\lim }\limits_{x \to + \infty } y = \mathop {\lim }\limits_{x \to - \infty } y = \frac{{{x^2} + 2x - 1}}{{{x^2} + 1}} = 1\). Do đó đường thẳng \(y = 1\) là một đường tiệm cận ngang của đồ thị hàm số \(y = \frac{{{x^2} + 2x - 1}}{{{x^2} + 1}}\). Vậy đồ thị hàm số \(y = \frac{{{x^2} + 2x - 1}}{{{x^2} + 1}}\) là hình 18b.