Tham khảo:
Theo định lí cosin ta có:
\(\begin{array}{l}{a^2} = {b^2} + {c^2} - \,2b\,c.\cos A\\{b^2} = {a^2} + {c^2} - \,2a\,c.\cos B\\{c^2} = {b^2} + {a^2} - \,2ab.\cos C\end{array}\)
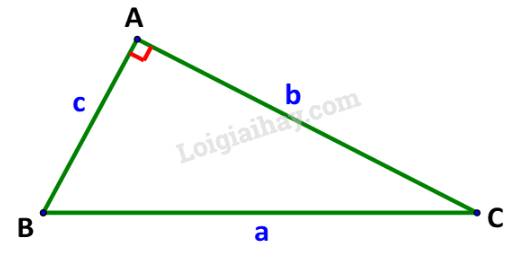
Mà \(\cos A = \cos {90^o} = 0;\cos B = \frac{c}{a};\;\cos C = \frac{b}{a}\)
\( \Rightarrow \left\{ \begin{array}{l}{a^2} = {b^2} + {c^2} - \,2b\,c.0\\{b^2} = {a^2} + {c^2} - \,2a\,c.\frac{c}{a}\\{c^2} = {b^2} + {a^2} - \,2ab.\frac{b}{a}\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}{a^2} = {b^2} + {c^2}\\{b^2} = {a^2} + {c^2} - \,2{a^2}\\{c^2} = {b^2} + {a^2} - \,2{b^2}\end{array} \right. \Leftrightarrow {a^2} = {b^2} + {c^2}\)
Vậy định lí Pythagore là một trường hợp đặc biệt của định lí cosin.