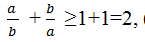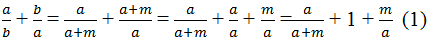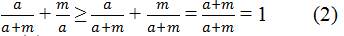Gọi phân số dương là \(\dfrac{a}{b}\) . ( Không mất tính tổng quát )
Cho \(a>0,\) \(b>0\) và \(a\ge b\) . Ta có thể viết \(a=b+m\left(m\ge0\right)\) .
Ta có:
\(\dfrac{a}{b}+\dfrac{b}{a}=\dfrac{b+m}{b}+\dfrac{b}{b+m}=1+\dfrac{m}{b}\ge1+\dfrac{m}{b+m}+\dfrac{b}{b+m}=1+\dfrac{m+b}{b+m}=2\)\(\Rightarrow\dfrac{a}{b}+\dfrac{b}{a}\ge2\)
Dấu đẳng thức xảy ra khi \(a=b\left(m=0\right)\)
Gọi a/b với a > 0, b > 0 là phân số đã cho và b/a là phân số nghịch đảo của nó . Không mất tính tổng quát giả sử 0 < a ≤ b.
Đặt b = a + m (m ∈ Z, m ≥ 0)
Ta có:
Và 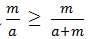
Suy ra:
Từ (1) và (2) suy ra: