Question

Chứng minh rằng nếu một điểm thuộc đường tròn (O) thì:

a) Điểm đối xứng với nó qua tâm O cũng thuộc (O).

b) Điểm đối xứng với nó qua một đường thẳng d tùy ý đi qua O cũng thuộc (O).

Answer 1

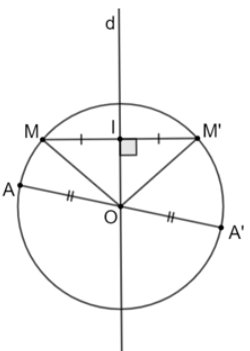
a) Lấy điểm A bất kì thuộc (O).

Gọi A' là điểm đối xứng với A qua O.

Khi đó: O là trung điểm của AA' hay OA = OA' = R.

Suy ra A' cũng thuộc đường tròn (O).

b) Lấy điểm M bất kì thuộc (O).

Gọi M' là điểm đối xứng với M qua d.

Gọi I là giao điểm của d với MM'.

Khi đó: MM' ⊥ OI tại M hay \(\widehat{OIM}=\widehat{OIM'}=90^o\)

Xét ∆OIM và ∆OIM' có:

OI chung

\(\widehat{OIM}=\widehat{OIM'}=90^o\)

IM = IM'

Do đó ∆OIM = ∆OIM' (c.g.c).