Bài 4: Khái niệm hai tam giác đồng dạng
Các câu hỏi tương tự
1) Cho tu giac ABCD co AB=2,5cm; AD=4cm; BD=5cm; BC=8cm; CD=10cm. CMinh ABCD la hinh thang
3) Cho tam giac ABC co AB=4cm, D thuoc AC, AD=2cm, DC=6cm. Biet goc A=100, goc B-C=20. Tinh goc ABD
cho hình thang ABCD có AB=3cm, BC= 10cm, CD=12cm, AD= 5cm, BD= 6cm
C/m ΔABC đồng dạng vs ΔBDC
có vẽ hình
Cho hình thang ABCD có AB = AD = 1/2 CD. Gọi M là trung điểm của CD. Gọi H là gia điểm của AM và BD.
a) Chứng minh tứ giác ABMD là hình thoi
b) Chứng minh DB vuông góc BC
c) CM: tam giác ADH đồng dạng với tamn giác CDB
d) Biết AB=2,5cm;BD=4cm. Tính độ dài cạnh BC và diện tích hình thang ABCD
giúp mk vs
Câu 7. Cho hình thang ABCD (AB//CD) có AB = 4cm; AD =8cm; BD = 10cm và 𝐷𝐴𝐵̂=𝐷𝐵𝐶̂. Tính độ dài các cạnh BC và CD lần lượt là:
giải giumd mìk cái =)
Cho tứ giác ABCD có đường chéo BD chia tứ giác đó thành hai tam giác đồng dạng là tam giác ABD đồng dạng với tam giác BDC
a) cmr AB song song với CD
b) Tính các độ dài BD, BC biết AB=2cm , AD=3cm , CD=8cm
Giup minh voi
Cho hình thang ABCD (AB//CD). Gọi O là giao điểm của hai đường chéo AC và BD. Qua O kẻ đường thẳng d song song với AB, d cắt AD và BC theo thứ tự ở M và N
a)Chứng minh AM/AD=BN/BC
b)Chứng minh OM=ONv
Hình thang ABCD (AB//CD) có CD = 2AB. Gọi E là trung điểm của DC (h.21).
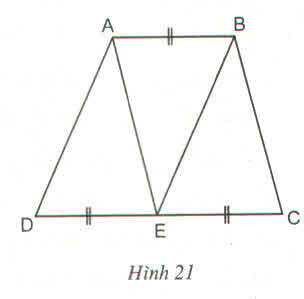
Chứng minh rằng 3 tam giác ADE, ABE và BEC đồng dạng với nhau từng đôi một. (Chú ý viết các đỉnh của hai tam giác đồng dạng theo thứ tự tương ứng với nhau)
hình thang ABCD(AB//CD)EG//AB//CD,AE=2/5 ED.
a,Tnhs BG/GC và CG/BC
b.tính EG biết AB=5cm và DC=30cm
cho hình thoi ABCD có A=60. Trên AB lấy điểm E soa cho AE<EB, trên AD lấy điểm F sao cho DF<AF. Qua E kẻ đường thẳng song song AC cắt BC tại G, qua F kẻ đường thẳng song song với AC cắt CD tại H. Chứng minh rằng:
a) Các tam giác BAD và DCB đều
b) Tứ giác EFGH là hình thang cân










