Question

Cho trục số được vẽ trên lưới ô vuông đơn vị như Hình 1.

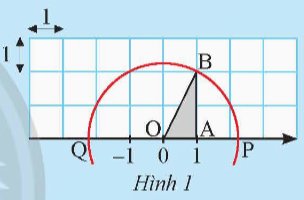
a) Tính độ dài cạnh huyền OB của tam giác vuông OAB.

b) Vẽ đường tròn tâm O bán kính OB, đường tròn này cắt trục số tại hai điểm P và Q.

Gọi x là số thực được biểu diễn bởi P, y là số thực được biểu diễn bởi Q.

Thay mỗi ? bằng số thích hợp để có các đẳng thức:

x² = ?; y² = ?.

Answer 1

a) Áp dụng định lí Pythagore vào tam giác vuông OAB ta có:

OB = \(\sqrt {1 + {2^2}}  = \sqrt 5 \)

b) Vì P, Q là hai điểm thuộc đường tròn tâm O bán kính OB nên \(OP = OQ = OB = \sqrt 5 \)

Vì x là số thực được biểu diễn bởi điểm P nên \(x = \sqrt 5 \),

y là số thực được biểu diễn bởi điểm Q nên \(y = -\sqrt 5 \).

Khi đó ta có các đẳng thức:

\({x^2} = {\left( {\sqrt 5 } \right)^2} = 5\)

\({y^2} = {\left( {-\sqrt 5 } \right)^2} = 5\)