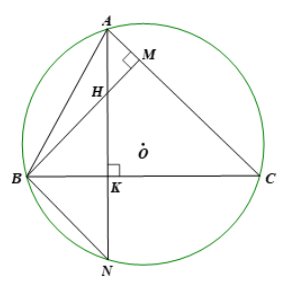
a) Xét tam giác ABC có đường cao AK, BM nên \(\widehat {AKC} = \widehat {BMC} = 90^\circ .\)
Xét tam giác BMC vuông tại M có: \(\widehat {CBM} + \widehat {BCA} = 90^\circ \)
Xét tam giác AKC vuông tại K có: \(\widehat {KAC} + \widehat {BCA} = 90^\circ \)
Nên \(\widehat {CBM} = \widehat {KAC}.\)
b) Xét tứ giác HKCM có:
\(\begin{array}{l}\widehat {HKC} + \widehat {HMC} + \widehat {KHM} + \widehat {KCM} = 360^\circ \\\widehat {KHM} + \widehat {KCM} = 360^\circ - \widehat {HKC} - \widehat {HMC}\\\widehat {KHM} + \widehat {KCM} = 360^\circ - 90^\circ - 90^\circ \\\widehat {KHM} + \widehat {KCM} = 180^\circ \end{array}\)
Mà \(\widehat {KHM} + \widehat {BHN} = 180^\circ \), suy ra \(\widehat {KCM} = \widehat {BHN}\) (1)
Ta lại có: \(\widehat {KCM} = \widehat {BNA}\)(2 góc nội tiếp cùng chắn cung AB của (O)) (2)
Từ (1) và (2) suy ra \(\widehat {BHN} = {\widehat {BNA}^{}}( = \widehat {KCM}).\)
Vậy tam giác BHN cân tại B.
c) Có: \(\widehat {BNC} = {\widehat {KAC}^{}}\)(2 góc nội tiếp cùng chắn cung NC của (O)).
Mà \(\widehat {CBM} = \widehat {KAC}\) (câu a)
Suy ra \(\widehat {CBM} = \widehat {BNC}\) hay BC là tia phân giác của góc NBH, do đó BK là đường phân giác của tam giác BNH.
Xét tam giác cân BNH có BK là đường phân giác nên BK đồng thời là đường trung trực hay BC là đường trung trục cua HN.
Vậy BC là đường trung trực của HN.


