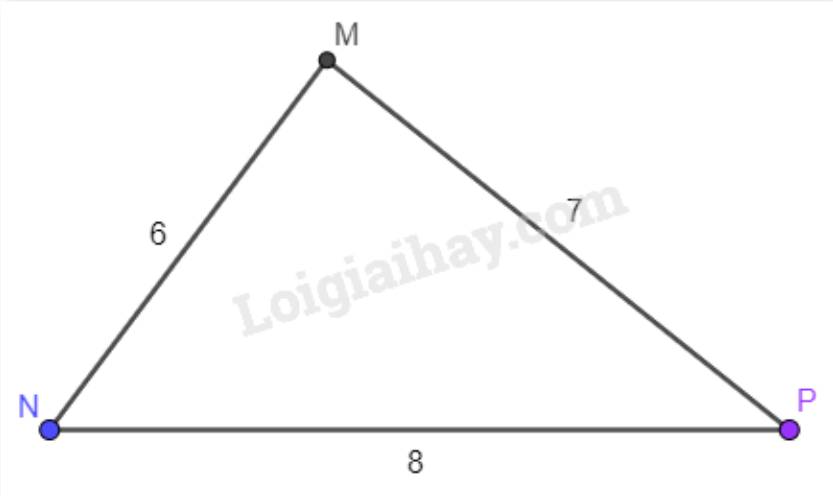
Trong tam giác MNP ta có: \(MN < MP < NP\) (6 < 7 < 8).
Vậy góc lớn nhất trong tam giác MNP là góc M (đối diện với cạnh NP) và góc nhỏ nhất trong tam giác MNP là góc P (đối diện với cạnh MN).

Trong tam giác MNP ta có: \(MN < MP < NP\) (6 < 7 < 8).
Vậy góc lớn nhất trong tam giác MNP là góc M (đối diện với cạnh NP) và góc nhỏ nhất trong tam giác MNP là góc P (đối diện với cạnh MN).
Cho tam giác MNP có \(MN = 4\)cm, \(NP = 5\)cm, \(MP = 6\) cm. Tìm góc nhỏ nhất, góc lớn nhất của tam giác MNP.
a) Cho tam giác DEG có góc E là góc tù. So sánh DE và DG.
b) Cho tam giác MNP có \(\widehat M = 56^\circ \), \(\widehat N = 65^\circ \). Tìm cạnh nhỏ nhất, cạnh lớn nhất của tam giác MNP.
Có hay không một tam giác mà độ dài ba cạnh của tam giác đó được cho bởi các độ dài trong mỗi trường hợp sau?
a) 8 cm, 5 cm, 3 cm;
b) 12 cm, 6 cm, 6 cm;
c) 15 cm, 9 cm, 4 cm.
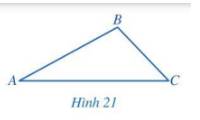
Bạn Thảo cho rằng tam giác ABC trong Hình 21 có \(AB = 3\)cm, \(BC = 2\)cm, \(AC = 4\)cm.
Cho tam giác ABC có \(AB = 2\)cm, \(BC = 4\)cm. So sánh hai cạnh AC và AB.
Quan sát tam giác ABC ở Hình 19.
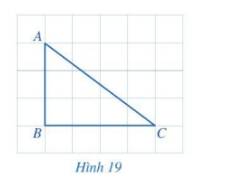
a) So sánh hai góc B và C.
b) So sánh cạnh AB (đối diện với góc C) và cạnh AC (đối diện với góc B).
Quan sát tam giác ABC ở Hình 17.
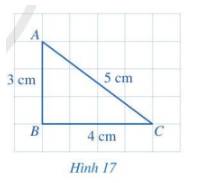
a) So sánh hai cạnh AB và AC.
b) So sánh góc B (đối diện với cạnh AC) và góc C (đối diện với cạnh AB).
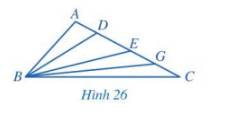
Cho tam giác ABC có góc A tù. Trên cạnh AC lần lượt lấy các điểm D, E, G sao cho D nằm giữa A và E; E nằm giữa D và G; G nằm giữa E và C (Hình 26). Sắp xếp các đoạn thẳng BA, BD, BE, BG, BC theo thứ tự tăng dần. Giải thích vì sao?
Bạn An có hai con đường đi từ nhà đến trường. Đường đi thứ nhất là đường đi thẳng từ nhà đến trường, đường đi thứ hai là đường đi thẳng từ nhà đến hiệu sách rồi đi thẳng từ hiệu sách đến trường (Hình 20). Theo em, bạn An đi từ nhà đến trường theo đường nào sẽ gần hơn?