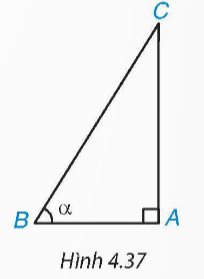
a) Ta có \(\sin \alpha = \frac{{AC}}{{BC}};\cos \alpha = \frac{{AB}}{{BC}}\)
b) Tam giác ABC vuông tại A nên ta có: \(A{B^2} + A{C^2} = B{C^2}\) (định lý Pythagore)
Nên ta có
\({\sin ^2}\alpha + {\cos ^2}\alpha = {\left( {\frac{{AC}}{{BC}}} \right)^2} + {\left( {\frac{{AB}}{{AC}}} \right)^2} = \frac{{A{C^2} + A{B^2}}}{{B{C^2}}} = \frac{{B{C^2}}}{{B{C^2}}} = 1\) (đpcm).
Đúng 0
Bình luận (0)