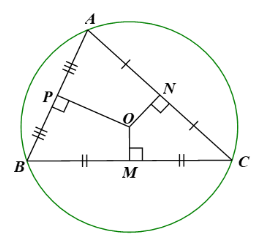
\(\Delta \)AOB có \(OA = OB\) (bán kính đường tròn (O)) nên \(\Delta \)OAB cân tại O, OP là đường trung tuyến đồng thời là đường cao. Suy ra: \(OP \bot AB\) nên \(\Delta \)OPA vuông tại P và \(\Delta \)OBP vuông tại P.
Chứng minh tương tự ta có: \(\Delta \)MOB vuông tại M, \(\Delta \)COM vuông tại M, \(\Delta \)NOC vuông tại N, \(\Delta \)NOA vuông tại N.
Vì \(\Delta \)OPA vuông tại P nên P thuộc đường tròn đường kính AO, \(\Delta \)NOA vuông tại N nên N thuộc đường tròn đường kính AO. Do đó, tứ giác ANOP nội tiếp đường tròn đường kính AO.
Vì \(\Delta \)OPB vuông tại P nên P thuộc đường tròn đường kính BO, \(\Delta \)MOB vuông tại M nên M thuộc đường tròn đường kính BO. Do đó, tứ giác BPOM nội tiếp đường tròn đường kính BO.
Vì \(\Delta \)COM vuông tại M nên M thuộc đường tròn đường kính CO, \(\Delta \)NOC vuông tại N nên N thuộc đường tròn đường kính CO. Do đó, tứ giác CMON nội tiếp đường tròn đường kính CO.


