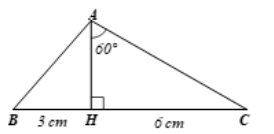
Cạnh \(BC = BH + HC = 3 + 6 = 9\) cm
Ta có:
\(\sin \widehat {HAC} = \frac{{HC}}{{AC}}\) hay \(\sin {60^0} = \frac{6}{{AC}}\) hay \(AC = \frac{6}{{\sin {{60}^0}}} = 4\sqrt 3 \approx 7\) cm
\(\tan \widehat {HAC} = \frac{{HC}}{{AH}}\) hay \(\tan {60^0} = \frac{6}{{AH}}\) nên \(AH = \frac{6}{{\tan {{60}^0}}} = 2\sqrt 3 \) cm
\(\widehat C = 90^\circ - 60^\circ = 30^\circ\)
Tam giác ABH vuông tại H nên ta có:
\(A{B^2} = A{H^2} + B{H^2} = {\left( {2\sqrt 3 } \right)^2} + {3^2} = 21\) hay \(AB = \sqrt {21} \approx 5\) cm (vì \(AB > 0\))
Ta có: \(tan B = \frac{AH}{BH} = \frac{2\sqrt 3}{3}\) suy ra \( \widehat B \approx 49^\circ\)
Áp dụng định lí tổng ba góc trong một tam giác, ta có:
\(\widehat {BAC} = 180^\circ - (\widehat B + \widehat C) = 180^\circ - (49^\circ + 30^\circ) = 101^\circ\)


