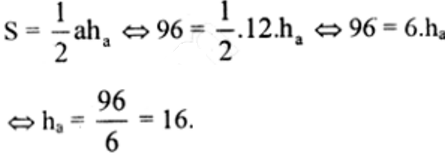Ôn tập chương II
Các câu hỏi tương tự
Cho tam giác ABC có \(a=12,b=16,c=20\)
a) Tính diện tích S và chiều cao \(h_a\)của tam giác
b) Tính độ dài đường trung tuyến \(m_a\) của tam giác
c) Tính bán kính \(R\) và \(r\) của các đường tròn ngoại tiếp và nội tiếp tam giác
Tam giác ABC có \(\widehat{A}=60^0;b=20;c=35\)
a) Tính chiều cao \(h_a\) ?
b) Tính bán kính đường tròn ngoại tiếp tam giác ?
c) Tính bán kính đường tròn nội tiếp tam giác ?
Cho tam giác ABC có a = 13, b = 14, c = 15
a) Tính diện tích tam giác ABC
b) Tính cos B, góc B nhọn hay tù
c) Tính bán kính đường tròn ngoại tiếp và nội tiếp của tam giác
d) Tính độ dài trung tuyến \(m_b\)
Cho tam giác ABC với AC = 13 cm, AB = 7 cm, BC = 15 cm. Tính B, bán kính đường tròn ngoại tiếp tam giác ABC và độ dài đường cao BH.
Tam giác ABC có cạnh \(BC=2\sqrt{3}\), cạnh \(AC=2\) và \(\widehat{C}=30^0\)
a) Tính cạnh AB và sin A
b) Tính diện tích S của tam giác ABC
c) Tính chiều cao \(h_a\) và trung tuyến \(m_a\)
cho tam giác ABC với A<3,1> ,B<-1,-1> , C <6,0>
a, tính AB*AC
b, tính diện tích tam giác ABC
c, tìm tọa độ trực tâm H của tam giác ABC
d, tìm tọa độ trọng tâm G của tam giác ABC
e, tìm tọa độ tâm I của đường tròn ngoại tiếp tam giác ABC từ đó chứng minh rằng I,H,G thẳng hàng
Chứng minh rằng với mọi tam giác ABC, ta có \(a=2R\sin A\), \(b=2R\sin B;c=2R\sin C\), trong đó R là bán kính đường tròn ngoại tiếp tam giác ?
Cho tam giác ABC có \(\widehat{A}=60^0;BC=6\). Tính bán kính đường tròn ngoại tiếp tam giác đó ?
Cho tam giác ABC có widehat{BAC}60^0;AB4;AC6
a) Tính tích vô hướng overrightarrow{AB}.overrightarrow{AC};overrightarrow{AB}.overrightarrow{BC}, độ dài cạnh BC và bán kính R của đường tròn ngoại tiếp tam giác ABC
b) Lấy các điểm M, N định bởi : 2overrightarrow{AM}+3overrightarrow{MC}overrightarrow{0};overrightarrow{NB}+xoverrightarrow{BC}overrightarrow{0};left(xne-1right). Định x để AN vuông góc với BM ?
Đọc tiếp
Cho tam giác ABC có \(\widehat{BAC}=60^0;AB=4;AC=6\)
a) Tính tích vô hướng \(\overrightarrow{AB}.\overrightarrow{AC};\overrightarrow{AB}.\overrightarrow{BC}\), độ dài cạnh BC và bán kính R của đường tròn ngoại tiếp tam giác ABC
b) Lấy các điểm M, N định bởi : \(2\overrightarrow{AM}+3\overrightarrow{MC}=\overrightarrow{0};\overrightarrow{NB}+x\overrightarrow{BC}=\overrightarrow{0};\left(x\ne-1\right)\). Định \(x\) để AN vuông góc với BM ?