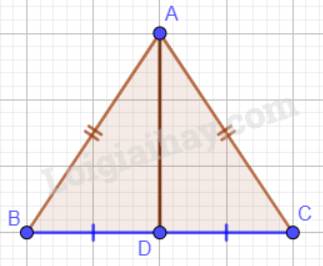
AD là phân giác của góc A nên \(\widehat {BAD} = \widehat {CAD}\).
Xét tam giác ABD và tam giác ACD có:
AB = AC (tam giác ABC cân tại A);
\(\widehat {BAD} = \widehat {CAD}\);
AD chung
Vậy \(\Delta ABD = \Delta ACD\)(c.g.c) nên \(BD = CD\) (2 cạnh tương ứng)
\(\Rightarrow\) D là trung điểm của cạnh BC.
Vì \(\Delta ABD = \Delta ACD\) nên \(\widehat {ADB} = \widehat {ADC}\) ( 2 góc tương ứng).
Mà \(\widehat {ADB} + \widehat {ADC}=180^0\) (2 góc kề bù) nên \(\widehat {ADB} = \widehat {ADC} = 90^\circ \Rightarrow AD \bot BC\).
Vậy AD là đường trung trực của tam giác ABC.