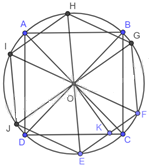
Gọi hình vuông ABCD và lục giác đều EFGHIJ cùng nội tiếp đường tròn (O).
Áp dụng định lí Pythagore vào tam giác ABC vuông tại B có:
\(A{C^2} = A{B^2} + B{C^2} \Rightarrow AC = \sqrt {A{B^2} + B{C^2}} = 3\sqrt 2 \left( {cm} \right)\)
Do đó, bán kính đường tròn (O) bằng \(\frac{{3\sqrt 2 }}{2}cm\).
Vì EFGHIJ là lục giác đều \(EF = FG = GH = HI = IJ = JE\)
Mà lục giác EFGHIJ nội tiếp (O) nên \(OE = OF = OG = OH = OI = OJ\).
Do đó, \(\Delta EOF = \Delta GOF = \Delta GOH = \Delta IOH = \Delta IOJ = \Delta EOJ\left( {c.c.c} \right)\)
Suy ra, \(\widehat {EOF} = \widehat {FOG} = \widehat {GOH} = \widehat {HOI} = \widehat {IOJ} = \widehat {JOE} = \frac{{{{360}^o}}}{6} = {60^o}\)
Tam giác EOF có: \(OE = OF,\widehat {EOF} = {60^o}\) nên tam giác EOF đều.
Do đó, \(OE = EF = \frac{{3\sqrt 2 }}{2}cm\)
Chu vi lục giác đều EFGHIJ là: \(P = 6EF = 6.\frac{{3\sqrt 2 }}{2} = 9\sqrt 2 \left( {cm} \right)\)
Kẻ OK vuông góc với EF tại K. Khi đó, OK là đường trung tuyến trong tam giác đều EOF.
Suy ra: \(EK = \frac{1}{2}EF = \frac{{3\sqrt 2 }}{4}cm\)
Áp dụng định lí Pythagore vào tam giác OKE vuông tại K có:
\(O{K^2} + K{E^2} = O{E^2} \Rightarrow OK = \sqrt {O{E^2} - K{E^2}} = \frac{{3\sqrt 6 }}{4}\left( {cm} \right)\)
Diện tích tam giác EOF là:
\({S_{EOF}} = \frac{1}{2}OK.EF = \frac{1}{2}.\frac{{3\sqrt 6 }}{4}.\frac{{3\sqrt 2 }}{2} = \frac{{9\sqrt 3 }}{8}\left( {c{m^2}} \right)\)
Vì \(\Delta EOF = \Delta GOF = \Delta GOH = \Delta IOH = \Delta IOJ = \Delta EOJ\) nên
\({S_{EFGHIJ}} = 6{S_{\Delta EOF}} = 6.\frac{{9\sqrt 3 }}{8} = \frac{{27\sqrt 3 }}{4}\left( {c{m^2}} \right)\)


