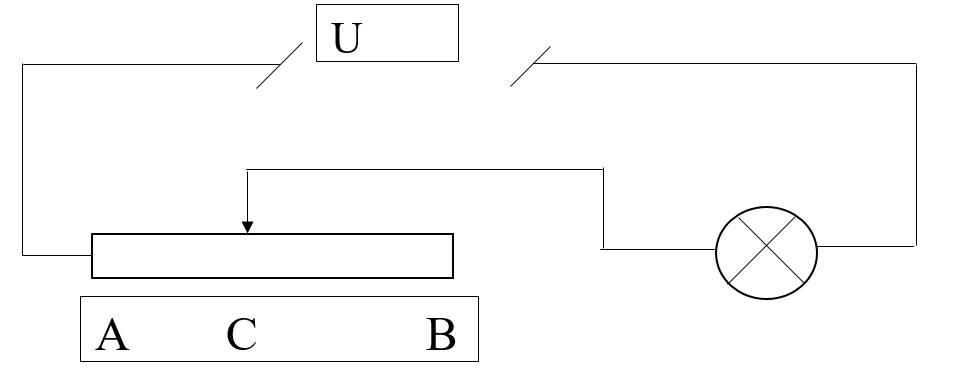
Cho mạch điện như hình vẽ,trong đó hiệu điện thế U=10.8V luôn không đổi, R1= 12Ω, đèn Đ có ghi 6V - 6W. Biến trở là một dây đồng chất, tiết diện đều có điện trở toàn phần Rb= 36Ω. Coi điện trở của đèn không đổi và không phụ thuộc vào nhiệt độ, điện trở của dây nối không đáng kể.
a, Điều chỉnh con chạy C sao cho phần biến trở RAC= 24Ω. Tìm:
- Rtương đương của đoạn mạch AB
- Cường độ dòng điện qua đèn và nhiệt lượng đèn tỏa ra trên R1 trong thời gian t=10 phút
b, Điều chỉnh con chạy C để đèn sáng bình thường, hỏi con chạy C đã chia biến trở thành hai phần có tỉ lệ như thế nào?
Rđ = 6^2/6 = 6
iều chỉnh con chạy C của biến trở để RAC = 24
=> \(R_{BC}=36-24=12\Omega\)
Mạch điện khi đó là
(R1//RAC)nt(RBC//RĐ)
\(R_{tđ}=\frac{R_1.R_{AC}}{R_1+R_{AC}}+\frac{R_đ.R_{BC}}{R_đ+R_{BC}}\)
\(=\frac{12.24}{12+24}+\frac{12.6}{12+6}=12\Omega\)
\(I=\frac{U}{R_{TĐ}}=\frac{10,8}{12}=0,9A\)
\(I_{1AC}=0,9A=>U_1=U_{AC}=0,9.8=7,2V\)
\(I_1=\frac{U_1}{R_1}=\frac{7,2}{12}=0,6A\)
\(Q_{1\left(10'\right)}=I_1^2R_1t=2592J\)
b, gọi vị trí để đèn sáng bình thường
RAC=x => RBC = 36-x
\(R_{tđ}=\frac{12x}{12+x}+\frac{6\left(36-x\right)}{6+36-x}=\frac{12x\left(42-x\right)+6\left(36-x\right)\left(12+x\right)}{\left(12+x\right)\left(42-x\right)}\)
\(I=\frac{U}{R_{tđ}}=\frac{10,8\left(12+x\right)\left(42-x\right)}{12x\left(42-x\right)+6\left(36-x\right)\left(12+x\right)}\)
\(U_đ=U_{BC}=\frac{10,8.6\left(12+x\right)\left(36-x\right)}{12x\left(42-x\right)+6\left(36-x\right)\left(12+x\right)}\)
\(I_đ=\frac{10,8\left(12+x\right)\left(36-x\right)}{12x\left(42-x\right)+6\left(36-x\right)\left(12+x\right)}=1\)
\(==>x=6\)
Như vậy phải đặt biến trở sao cho RAC = 6 \(\Omega\)