Hiện tại là cái máy tính của tui nó không ở đây <cụ thể là mất trước tết>, vậy nên bro tự tính toán nha :(
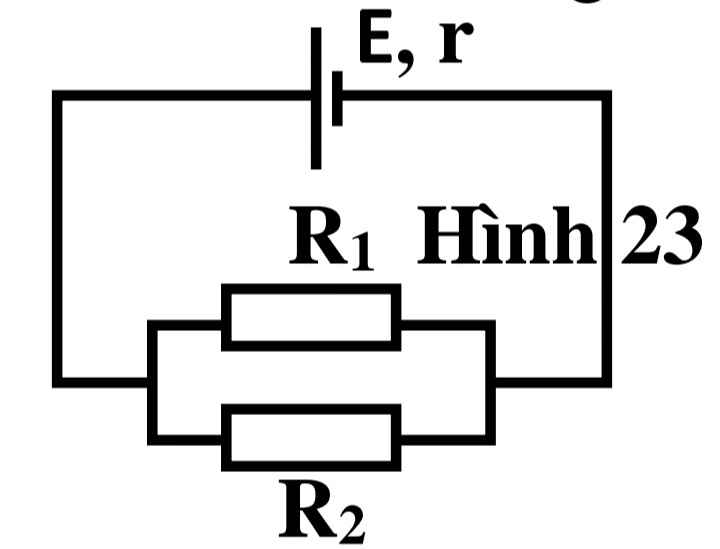
\(I=\frac{E}{r+R_1+R_2}\)
\(U_2=U_1=I.R_{12}=I.\frac{R_1R_2}{R_1+R_2}=\frac{E}{r+R_1+R_2}.\frac{R_1R_2}{R_1+R_2}\)
\(P_2=\frac{U^2_2}{R_2}=0,3\Leftrightarrow\frac{\left(\frac{E}{r+R_1+R_2}.\frac{R_1R_2}{R_1+R_2}\right)^2}{R_2}=0,3\)
Phương trình chỉ còn ẩn R2, bạn tự giải
\(P_{nguon}=I^2.r=\left(\frac{E}{r+R_1+R_2}.\frac{R_1R_2}{R_1+R_2}\right)^2.r=...\left(W\right)\)
Hiệu suất của nguồn sẽ bằng Hiệu điện thế mạch ngoài chia cho E: \(H=\frac{U_{mn}}{E}.100\%=\frac{U_1}{E}.100\%=...\)
b/ Câu này sử dụng biểu thức tui đã viết bên trên, tìm cách đưa tất cả R2 xuống mẫu, và lí luận rằng để công suất tiêu thụ của R2 là max thì mẫu phải min, từ đó sử dụng những bdt phù hợp để tìm min (tội quá, ko có máy tính nên lười tính chay lắm :( )