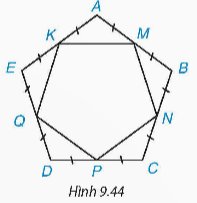
Vì ABCDE là ngũ giác đều nên \(AB = BC = CD = DE = EA\), \(\widehat A = \widehat B = \widehat C = \widehat D = \widehat E\)
Vì M, N, P, Q, K lần lượt là trung điểm của các cạnh AB, BC, CD, DE, EA.
Do đó, \(AM = MB = NB = NC = CP = PD = DQ = QE = EK = KA\)
Ta có: \(AM = MB = NB = NC = CP = PD = DQ = QE = EK = KA\) và \(\widehat A = \widehat B = \widehat C = \widehat D = \widehat E\)
Suy ra: \(\Delta AMK = \Delta BMN = \Delta CPN = \Delta DPQ = \Delta EKQ\left( {c.g.c} \right)\)
Do đó: + \(KM = MN = PN = PQ = QK\left( 1 \right)\).
+ \(\widehat {KMA} = \widehat {AKM} = \widehat {BMN} = \widehat {MNB} = \widehat {CNP} = \widehat {CPN} = \widehat {DPQ} = \widehat {DQP} = \widehat {EQK} = \widehat {EKQ}\)
Ta có: \(\widehat {KMA} + \widehat {KMN} + \widehat {BMN} = {180^o}\) (các góc kề bù)
Mà \(\widehat {KMA} = \widehat {BMN}\) nên \(\widehat {KMN} = {180^o} - 2\widehat {KMA}\).
Vì \(\widehat {BNM} + \widehat {MNP} + \widehat {PNC} = {180^o}\) (các góc kề bù)
Mà \(\widehat {KMA} = \widehat {BNM} = \widehat {PNC}\) nên \(\widehat {MNP} = {180^o} - 2\widehat {KMA}\).
Chứng minh tương tự ta có:
\(\widehat {NPQ} = \widehat {PQK} = \widehat {QKM} = {180^o} - 2\widehat {KMA}\)
Do đó, \(\widehat {KMN} = \widehat {MNP} = \widehat {NPQ} = \widehat {PQK} = \widehat {QKM}\left( 2 \right)\)
Từ (1) và (2) suy ra: MNPQK là ngũ giác đều.