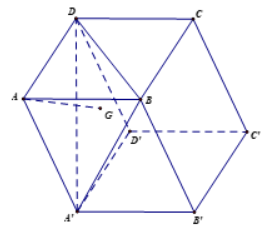
a) Vì G là trọng tâm của tam giác BDA' nên
$$
\begin{aligned}
& \overrightarrow{G B}+\overrightarrow{G D}+\overrightarrow{G A^{\prime}}=\overrightarrow{0} \\
& \Leftrightarrow \overrightarrow{G A}+\overrightarrow{A B}+\overrightarrow{G A}+\overrightarrow{A D}+\overrightarrow{G A}+\overrightarrow{A A^{\prime}}=\overrightarrow{0} \\
& \Leftrightarrow 3 \overrightarrow{G A}+\overrightarrow{A B}+\overrightarrow{A D}+\overrightarrow{A A^{\prime}}=\overrightarrow{0} \\
& \Leftrightarrow \overrightarrow{A G}=\frac{1}{3}\left(\overrightarrow{A B}+\overrightarrow{A D}+\overrightarrow{A A^{\prime}}\right)
\end{aligned}
$$
b) Vì $A B C D . A^{\prime} B^{\prime} C^{\prime} D^{\prime}$ là hình hộp nên theo quy tắc hình hộp ta có:
$$
\overrightarrow{A C^{\prime}}=\overrightarrow{A B}+\overrightarrow{A D}+\overrightarrow{A A^{\prime}}(2)
$$
Từ (1) và (2), ta có $\overrightarrow{A G}=\frac{1}{3} \overrightarrow{A C^{\prime}}$.
Vậy ba điểm $\mathrm{A}, \mathrm{G}$ và C' thẳng hàng.


