Bài 2: Diện tích hình chữ nhật
Các câu hỏi tương tự
Cho hình chữ nhật ABCD với AB = 8cm, đường chéo BD = 10cm. Gọi H là chân đường góc kẻ từ A đến BD. Gọi M và N lần lượt là trung điểm của các đoạn AH và DH.
a) Chứng minh rằng MN//AD
b) Tính diện tích ABCD
Giúp mình mai mình thi rồi
Xem chi tiết
Cho tứ giác ABCD gọi M N P Q lần lượt là trung điểm của các cạnh AB BC CD DA
A) Chứng minh tứ giác MNPQ là hình bình hành
b) tìm điều kiện hai đường chéo AC và BD của tứ giác ABCD để MNPQ là hình chữ nhật
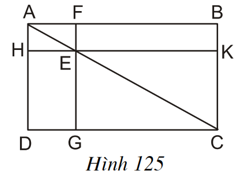
Cho hình 125, trong đó ABCD là hình chữ nhật, E là một điểm bất kì nằm trên đường chéo AC, FG // AD và HK // AB. Chứng minh rằng hai hình chữ nhật EFBK và EGDH có cùng diện tích.
Đọc tiếp
Cho hình 125, trong đó ABCD là hình chữ nhật, E là một điểm bất kì nằm trên đường chéo AC, FG // AD và HK // AB. Chứng minh rằng hai hình chữ nhật EFBK và EGDH có cùng diện tích.
Một hình thang cân có hai đường chéo vuông góc với nhau, độ dài đường
chéo bằng 6cm. Tính diện tích tứ giác có các đỉnh là trung điểm của các cạnh
của hình thang cân đó.
Cho hình 125:
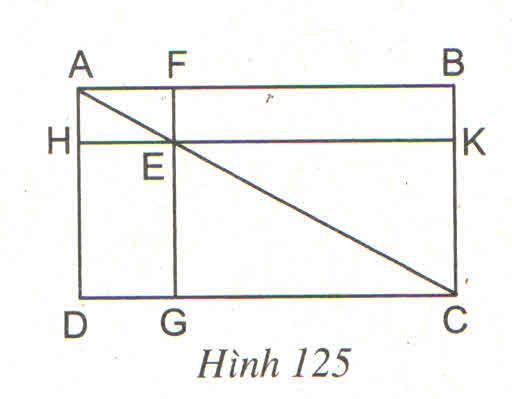
Trong đó ABCD là hình chữ nhật, E là một điểm bất kì nằm trên đường chéo AC, FG // AD và HK // AB
Chứng minh rằng hai hình chữ nhật EFBK và EGDH có cùng diện tích ?
Cho hình bình hành ABCD (h.183).

Từ A và C kẻ AH và CK vuông góc với đường chéo BD. Chứng minh rằng hai đa giác ABCH và ADCK có cùng diện tích ?
Cho hình chữ nhật ABCD có AB bằng 12 cm AD bằng 6,8 cm gọi H I K lần lượt là trung điểm của BC, HC, DC, AC tính diện tích DBE
Xem chi tiết
Cho hình chữ nhật ABCD. Gọi M,N,Q lần lượt là trung điểm của AB,BC,AC .
a. Chứng minh tứ giác BMQN là hình chữ nhật
b. Cho biết AB=12cm , AC=25cm . Tính diện tích tam giác ABC và diện tích hình chữ nhật ABCD
Cho hình bình hành ABCD. Đường phân giác của các góc A và C cắt đường chéo BD tại E và F

a) Chứng minh rằng hai hình ABCFE và ADCFE có cùng diện tích
b) Các hình đó có phải là đa giác lồi không ? Vì sao ?