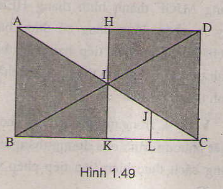
Phép vị tự tâm C tỉ số 2 biến hình thang JLKI thành hình thang IKBA. Phép đối xứng tâm I biến hình thang IKBA thành hình thang IHDC. Do đó hai hình thang JLKI và IHDC đồng dạng với nhau.
Bài 8. Phép đồng dạng
Đúng 0
Bình luận (0)
Các câu hỏi tương tự
Cho hình chữ nhật ABCD,có AC và BD cắt nhau tại I. Gọi điểm HKLJ ần lược là trung điểm cuẩD,BC,KC và IC. Tìm một phép biến hình biến hình thang IKNA thành hình thang JLKI
cho hình chữ nhật ABCD tâm I .các điểm M;N;P;Q;R lần lượt là trung điểm của AB;BC;CD;DA;MI.hai hình thang ARIQ và ANCD có đồng dạng với nhau không? Vì sao?
Cho hình thang ABCD có AB song song với CD, AD = a, DC = b còn hai đỉnh A, B cố định. Gọi I là giao điểm của hai đường chéo.
a) Tìm tập hợp các điểm C khi D thay đổi
b) Tìm tập hợp các điểm I khi C và D thay đổi như trong câu a)
Cho hình vuông ABCD, P thuộc cạnh AB , H là chân đường vuông góc hạ từ B đến PC . Phép đồng dạng biến \(\Delta\)BHC thành \(\Delta\)PHB . Khi đó ảnh của B và D là?
Chứng minh rằng hai đa giác đều có cùng số cạnh luôn đồng dạng với nhau ?
cho tam giac abc xác dịnh ảnh của nó qua phép đồng dạng bằng cách thực hiện liên tiếp phép vị tự tâm b tỉ số 1/2 và phép đối xứng qua đườn trung trực của bc
Cho tam giác ABC. Xác định ảnh của nó qua phép đồng dạng có được bằng cách thực hiên liên tiếp phép vị tự tâm B tỉ số \(\dfrac{1}{2}\) và phép đối xứng qua đường trung trực của BC ?
Cho tam giác ABC, gọi E và F theo thứ tự là hình chiếu của B và C trên tia phân giác AD của góc A. Gọi K là giao điểm của FB và CE. CM: a) AE.CF= BE.AF; b) BE//AK; c) AK là tia phân giác góc ngoài đỉnh A
Trong mặt phẳng Oxy cho điểm \(I\left(1;1\right)\) và đường tròn tâm I bán kính 2. Viết phương trình của đường tròn là ảnh của đường tròn trên qua phép đồng dạng có được bằng cách thực hiện liên tiếp phép quay tâm O, góc \(45^0\) và phép vị tự tâm I, tỉ số \(\sqrt{2}\) ?