Giải:
Quay quanh AB thì ta có r = a, h= 2a.
nên V1 = πr2h = π.a2.2a = 2πa3
Quay quanh BC thì ta có r = 2a, h = a
nên V2 = πr2h = π(2a)2.a = 4πa3
Do đó 2V1 = V2
Vậy chọn C
Giải:
Quay quanh AB thì ta có r = a, h= 2a.
nên V1 = πr2h = π.a2.2a = 2πa3
Quay quanh BC thì ta có r = 2a, h = a
nên V2 = πr2h = π(2a)2.a = 4πa3
Do đó 2V1 = V2
Vậy chọn C
Diện tích và chu vi của một hình chữ nhật ABCD (AB > AD) theo thứ tự là \(2a^2\) và \(6a\). Cho hình chữ nhật quay quanh cạnh AB một vòng, ta được một hình trụ. Tính thể tích và diện tích xung quanh của hình trụ này ?
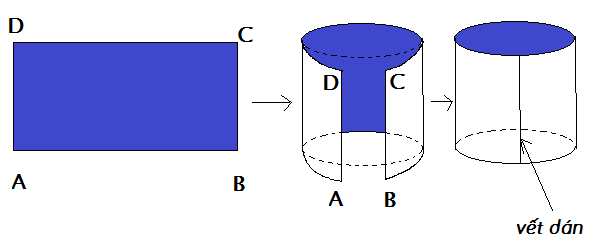
Lấy một băng giấy hình chữ nhật ABCD. Biết AB = 10 cm, BC = 4 cm; dán băng giấy như hình vẽ (B sát với A và C sát với D, không được xoắn).
Có thể dán băng giấy để tạo nên mặt xung quanh của hình trụ được không?
Từ một tấm tôn hình chữ nhật kích thước 40cm x 60cm người ta gò thành mặt xung quanh của một hình trụ có chiều cao 40cm. Tính thể tích của khối trụ đó
Cho hình trụ có bán kính đáy bằng 3cm và đường cao gấp đôi bán kính đáy a) tính S xung quanh của hình trụ b)tính S toàn phần của hình trụ c)tính thể tích của hình trụ
Câu 1: Thể tích hình trụ là 375 π , chiều cao 15. Tính diện tích xung quanh hình trụ.
Câu 2: Một hình trụ có diện tích toàn phần bằng diện tích hình tròn có bán kính 12cm, chiều cao hình trụ bằng 2 lần bán kính đáy. Tính bán kính đáy hình trụ đó.
Chiều cao của một hình trụ bằng bán kính đường tròn đáy. Diện tích xung quanh hình trụ là 314 cm2. Hãy tính bán kính đường tròn đáy và thể tích hình trụ (làm tròn kết quả đến chữ số thập phân thứ hai).
Một hình trụ có bán kính đường tròn đáy là 6cm, chiều cao 9cm. Hãy tính :
a) Diện tích xung quanh của hình trụ
b) Thể tích của hình trụ
(Lấy \(\pi=3,142\), làm tròn kết quả đến hàng đơn vị)
Hãy tính:
a) Diện tích xung quanh của một hình trụ có chu vi hình tròn đáy là 13 cm và chiều cao là 3 cm.
b) Thể tích của hình trụ có bán kính đường tròn đáy là 5 mm và chiểu cao là 8 mm.
cho hình trụ bán kính đáy là 3cm biết diện tích xung quanh hình trụ là 90 cm2 . tính thể tích hình trụ