Question

Cho hai đường tròn cùng tâm (O; R), (O; r) với R > r. Các điểm A, B thuộc đường tròn (O; R), các điểm A’ B’ thuộc đường tròn (O; r) sao cho O, A, A’ thẳng hàng; O, B, B’ thẳng hàng và điểm O không thuộc đường thẳng AB. Chứng minh:

a) \(\dfrac{OA'}{OA}=\dfrac{OB'}{OB}\);

b) AB // A’B’.

Answer 1

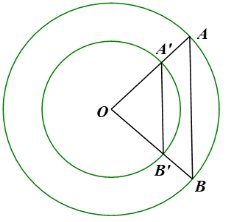
a) Ta có: $\frac{O A^{\prime}}{O A}=\frac{r}{R} ; \frac{O B^{\prime}}{O B}=\frac{r}{R}$, suy ra $\frac{O A^{\prime}}{O A}=\frac{O B^{\prime}}{O B}$.
b) Xét $\triangle \mathrm{OAB}$ có $\frac{O A^{\prime}}{O A}=\frac{O B^{\prime}}{O B}$ nên $\mathrm{AB} / / A^{\prime} B^{\prime}$ (theo định lí Thalès đảo).