Question

Cho góc xOy với đường phân giác Ot và điểm A trên cạnh Ox, điểm B trên cạnh Oy sao cho OA = OB. Đường thẳng qua A và vuông góc với Ox cắt Ot tại M. Chứng minh rằng OA và OB là hai tiếp tuyến cắt nhau của đường tròn (M; MA).

Answer 1

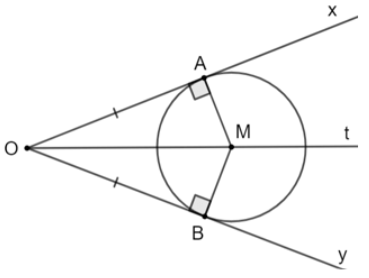
Ta có: OA là tiếp tuyến của đường tròn (P; PA) do OA \( \bot \) PA tại A.

Xét tam giác OAP và tam giác OBP có:

OP chung

\(\widehat {{\rm{AOP}}} = \widehat {{\rm{BOP}}}\) (do OP là tia phân giác của góc \(\widehat {{\rm{AOB}}}\))

OA = OB

Vậy \(\Delta {\rm{OAP}} = \Delta {\rm{OBP}}\) (c.g.c)

Suy ra: PA = PB (hai cạnh tương ứng)

\(\widehat {{\rm{OAP}}} = \widehat {{\rm{OBP}}} = 90^\circ \) (hai góc tương ứng) hay OB \( \bot \) PB

Do đó OA là tiếp tuyến của đường tròn (P; PA)

Vậy OA và OB là hai tiếp tuyến cắt nhau của (O).