Question

Cho góc xOy. Lấy hai điểm A, B thuộc tia Ox sao cho OA < OB. Lấy hai điểm C, D thuộc tia Oy sao cho OC = OA, OD = OB. Gọi E là giao điểm của AD và BC. Chứng minh rằng:

a) AD = BC

b) \(\Delta EAB=\Delta ECD\)

c) OE là tia phân giác của góc xOy.

Answer 1

Tham khảo:

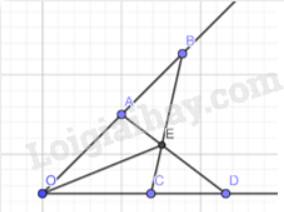
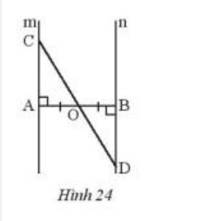
a) Xét \(\Delta OAD\) và \(\Delta OCB\), ta có :

OD = OB

\(\widehat{A}\) chung

OA = OC 

\(\Rightarrow \Delta OAD=\Delta OCB\) (c-g-c )

\( \Rightarrow AD = BC\)(2 cạnh tương ứng )

b) Vì \(\Delta OAD=\Delta OCB\) nên \(\widehat{OAD}=\widehat{OCB}; \widehat{D}=\widehat{B}\) ( 2 góc tương ứng)

Mà \(\widehat{OAD}+\widehat{BAD}=180^0\) ( 2 góc kề bù)

\(\widehat{OCB}+\widehat{BCD}=180^0\) ( 2 góc kề bù)

Do đó, \(\widehat{BAD}=\widehat{BCD}\)

Vì \(OA+AB=OB; OC+CD=OD\)

Mà \(OC = OA, OD = OB\)

\(\Rightarrow AB=CD\)

Xét \(\Delta EAB\) và \(\Delta ECD\), ta có:

\(\widehat {ABE} = \widehat {CDE}\)

\(AB = CD\)

\(\widehat {BAE} = \widehat {DCE}\)

\(\Rightarrow \Delta EAB=\Delta ECD\) (g-c-g)

c) Vì \(\Delta EAB=\Delta ECD\) nên EB = ED ( 2 cạnh tương ứng)

Xét \(\Delta OBE\) và \(\Delta ODE\), ta có :

 EB = ED

OB = OD

OE chung

\( \Rightarrow \Delta OBE=\Delta ODE \)  (c.c.c)

\( \Rightarrow \widehat{BOE}=\widehat{DOE}\) ( 2 góc tương ứng)

\( \Rightarrow \) OE là phân giác \(\widehat {xOy}\)