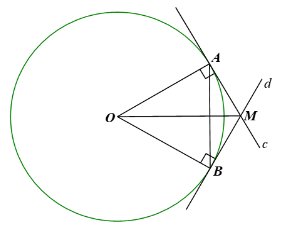
Vì \(MA,MB\) là các tiếp tuyến của \(\left( O \right)\) nên MO là tia phân giác của góc AMB, suy ra \(\widehat {AMO} = \widehat {BMO} = \frac{{\widehat {AMB}}}{2} = 60^\circ \).
Xét tam giác \(AMO\) vuông tại \(A\) có:
\(\widehat {AMO} + \widehat {MOA} = 90 \\60^\circ + \widehat {MOA} = 90^\circ \\ \widehat {MOA} = 30^\circ \)
Vì \(MA,MB\) là các tiếp tuyến của \(\left( O \right)\) nên OM là tia phân giác của góc AOB, suy ra \(\widehat {AOB} = 2\widehat {AOM} = 2.30^\circ = 60^\circ \).
Xét tam giác \(AOB\) có: \(OA = OB = R\) nên tam giác \(AOB\) cân tại \(O\).
Lại có \(\widehat {AOB} = 60^\circ \) suy ra tam giác \(AOB\) là tam giác đều.
Vậy \(AO = OB = AB = R\).