Question

Cho đường tròn (O) , điểm M nằm ngoài (O) sao cho hai tiếp tuyến MA và MB (A; B là hai tiếp điểm) thoả mãn \(\widehat {AMB} = {60^o}\). Biết chu vi tam giác MAB là 18 cm, tính độ dài dây AB.

Answer 1

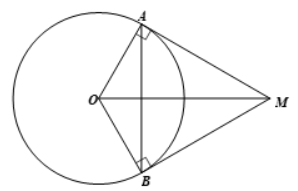
Vì AM, MB là hai tiếp tuyến suy ra \(MA \bot AO;MB \bot BO\).

Xét tam giác vuông AMO và tam giác vuông BMO có:

MO là cạnh chung

OA = OB

Suy ra \(\Delta \)AMO = \(\Delta \)BMO (cạnh huyền – cạnh góc vuông)

Nên MA = MB. Do đó tam giác MAB cân tại M.

Mặt khác, ta có: \(\widehat {AMB} = {60^o}\) nên tam giác MAB đều suy ra AB = MA = MB

Mà AB + AM + MB = \({P_{MAB}}\) = 18

Suy ra 3AB = 18 nên AB = 6 cm.