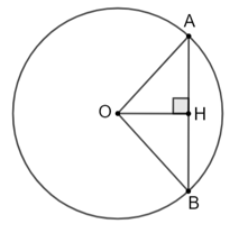
a) Vẽ bán kính OM của đường tròn, trên OM lấy điểm H sao cho OH = 2,5 cm. Kẻ đoạn thẳng AB vuông góc với OH tại H, cắt đường tròn tại A và B ta được dây cung AB cần vẽ.
b) Gọi H là trung điểm của AB.
Xét tam giác OAH và tam giác OBH có:
OA = OB = R
Cạnh OH chung
\(\widehat {OHA} = \widehat {OHB} = 90^\circ \)
\( \Rightarrow \Delta OAH = \Delta OBH\)(cạnh huyền – cạnh góc vuông)
\( \Rightarrow AH = BH\)(hai cạnh tương ứng) \( \Rightarrow AB = 2AH\)
Xét tam giác OAH vuông tại H có: \(A{H^2} + O{H^2} = O{A^2}\)(định lý Pythagore)
hay \(A{H^2} = O{A^2} - O{H^2} = {5^2} - 2,{5^2} = 18,75 \Rightarrow AH = \frac{5\sqrt 3}{2} \)(cm)
\( \Rightarrow AB = 2.\frac{5\sqrt 3}{2} = 5\sqrt 3 \approx 8,66\)(cm)
c) Xét tam giác OAH vuông tại H có: \(\cos \widehat {AOH} = \frac{{OH}}{{OA}} = \frac{{2,5}}{5} = \frac{1}{2} \Rightarrow \widehat {AOH} = 60^\circ \)
Mà: \(\Delta OAH = \Delta OBH\)\( \Rightarrow \widehat {BOH} = \widehat {AOH} = 60^\circ \)(hai góc tương ứng)
\( \Rightarrow \widehat {AOB} = \widehat {BOH} + \widehat {AOH} = 60^\circ + 60^\circ = 120^\circ \)
\( \Rightarrow \) sđ\(\overset\frown{AB}=120{}^\circ \)
Độ dài cung AB là: \(\frac{{120}}{{180}}.\pi .5 = \frac{{10}}{3}\pi \)(cm)
d) Diện tích hình quạt tròn ứng với cung nhỏ AB là: \(\frac{{{\rm{120}}}}{{{\rm{360}}}}{\rm{.\pi }}{\rm{.5^2 = }}\frac{{\rm{25\pi }}}{{{\rm{3}}}}\left( {{\rm{c}}{{\rm{m}}^{\rm{2}}}} \right)\)


